接下来,我们以概率的角度来看待分类问题,并说明模型如何从数据分布的简单假设来得到线性决策边界的。在1.5.4节中,我们讨论了分类中判别式和生成方法的区别。这里我们使用对类条件概率密度和类先验概率分布建模,并通过贝叶斯定理使用这些来计算后验概率的生成方法。
首先,考虑二分类的情形。类的后验概率可以写成
其中我们定义了
是定义成
的logistic sigmoid函数,如图4.9展示。
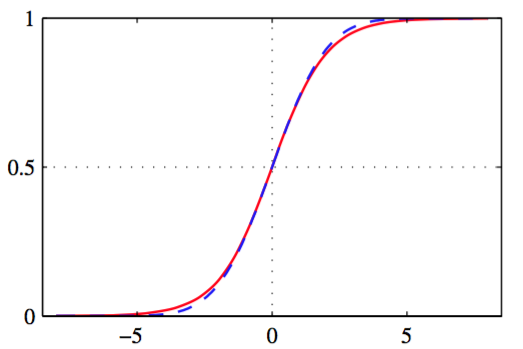
图 4.9 logistic sigmoid函数
“sigmoid”的意思是“S形”。由于这种函数把整个实数轴映射到了一个有限的区间中,所以它有时也被称为“压缩函数”。logistic sigmoid函数我们已经在之前的章节遇到过了,且在许多分类算法中都有着重要的作用。它满足对称性:
这很容易证明。logistic sigmoid的反函数由
给出,它被称为logit函数。表示两类的概率比值的对数被称为log odds函数。
注意,式(4.57)中我们简单的吧后验概率重写为等价的形式,这可能使得logistic sigmoid函数看上去没有意义。但是,它使得具有简单的函数形式。稍后,我们会考虑为的线性函数的情况,其中后验概率是由通用线性模型控制的。
对于个类别的情形,我们有
这被称为标准化指数,并可以被当做logistic sigmoid函数对于多类情况的推广。由
定义。标准化指数也被称为softmax函数。这是因为,如果对于所有的情况,都有的情况下,有。所以它表示“最大化”函数的一个平滑版本。
现在,我们探讨选择类条件密度的具体形式的结果,首先讨论连续输入变量的情形,然后简要地讨论离散输入的情形。