大部分应用中,我们的目标不会只是最小化误分类的数量这么简单。让我们再次考虑医学诊断问题。注意,如果误诊断病人患有癌症,后果是一些病人窘迫的进行进一步的诊断。相反的,如果误诊断病人未患癌症,那么他可能由于得不到治疗而过早的死亡。两种误分类导致的后果是完全不同的。很明显,即使会导致第一种误分率上升,越少的第二种误分数量越好。
通过引入损失函数(loss function)或成本函数(cost function)可以形式化这样的问题。它是对所有可能的决策或动作所产生的损失采用一种统一的整体度量。然后我们的目标是最小化整体的损失。一些作者使用最大化效用函数(utility function)来替代。如果让效用函数等于负的损失函数的话,那么它们是等价的,因此在本书中我们都将使用损失函数这个概念。假设新的值,它的实际类别是,但我们把它分到了中(其中可能等于也可能不等于),这样做之后会产生某种程度的损失,记作也就是损失矩阵(loss matrix)的第项。举个例子,图1.25展示了癌症例子的损失矩阵。
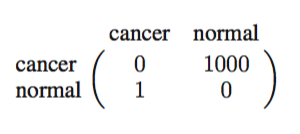
图 1.25: 损失矩阵
这个具体的损失矩阵表示对于正确的分类是不会产生损失的,对于误诊断为癌症时损失为1,误诊断为未患癌症时损失为1000。
最优解是最小化损失函数,然而,损失函数依赖于未知的正确类别。给定输入向量,对正确分类的不确定性由联合概率分布表示,所以用最小化平均损失来替代。关于这个分布的平均损失:
每一个可以被独立地分到决策区域中。目标是选择决策区域来最小化损失期望(1.80),这隐含了对于每个最小化。与之前一样可以是用乘法规则来消除公共项。所以,最小化损失期望的决策规则是对于每个新的,把它分到能使下式:
取得最小值的第类。当知道了类的后验概率之后就很容易了。