除了考虑离散事件的概率外，我们还希望考虑连续变量的概率。我们会把的讨论限制在一个相对非正式的形式上。如果一个实值变量$x$落在区间$(x, x + \delta x)$的概率由$p(x)\delta x$给出，其中$\delta x \to 0$，那么我们就把$p(x)$称作$x$的概率密度（probability density）。图1.12阐释了这个概念。$x$位于区间$(a, b)$的概率由下式给出:

$$p(x \in (a, b)) = \int_a^b p(x) dx \tag{1.24}$$

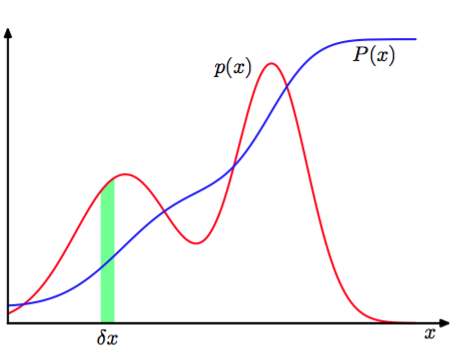
图 1.12: 连续变量的概率密度函数

因为概率是非负的，并且$x$的值必须在实轴上，所以概率密度$p(x)$必须满足这两个条件：

$$\begin{eqnarray} p(x) \geq 0 \tag{1.25} \\ \int_{-\infty}^{\infty} p(x) dx = 1 \tag{1.26} \end{eqnarray}$$

在变量的非线性变化下，概率密度由一个简单的函数通过Jacobian因子变换得到。例如：一个变量 $x = g(y)$，那么函数$f(x)$ 就变成 $\widetilde{f}(y) = f(g(y))$。现在，考虑概率密度$p_x(x)$，与它对应的关于新变量$y$的密度$p_y(y)$，其中不同的下标表示$p_x(x), p_y(y)$ 是不同的两个密度函数。观测区间$(x, x + \delta x)$变换为区间$(y, y + \delta y)$，当$\delta x$很小时，我们有$p_x(x)\delta x \simeq p_y(y)\delta y$ 即：

$$\begin{eqnarray} p_y(y) &=& p_x(x)\big|\frac{dx}{dy}\big| \\ &=& p_x(g(y))|g^\prime(y)| \tag{1.27} \end{eqnarray}$$

这个性质的一个结果就是：概率密度的最大值取决于变量的选择。

$x$位于区间$(-\infty, z)$的概率是由累计分布函数（cumulative distribution function）给出的：
$$P(z) = \int_{-\infty}^z p(x)dx \tag{1.28}$$

它就像图1.12那样满足$P^\prime(x) = p(x)$。

如果我们有几个连续变量$x_1,...,x_D$，一起被记作向量$x$，那么我们就定义：联合概率密度$p(x) = p(x_1,...,x_D)$是使得落在包含点$x$的无穷小体积$\delta x$的点的概率等于$p(x)\delta x$。多变量概率密度必须满足

$$\begin{eqnarray} p(x) \geq 0 \tag{1.29} \\ \int p(x) dx = 1\tag{1.30} \end{eqnarray}$$

其中积分必须包含整个$x$空间。这也适用于离散变量和连续变量相结合的联合概率分布。

注意：如果$x$是离散变量，那么$p(x)$就叫做概率质量函数（probability mass function），因为它可以被看做在合法的$x$值上的“概率质量”的集合。

概率的加法，乘法规则以及贝叶斯定理，都适用于概率密度或离散变量与连续变量相结合的情形下。例如：$x,y$是两个实值变量，它们的加法，乘法规则可以表示为如下形式：
$$\begin{eqnarray} p(x) &=& \int p(x, y) dy \tag{1.31} \\ p(x, y) &=& p(y|x)p(x) \tag{1.32} \end{eqnarray}$$

形式化地证明连续变量的加法，乘法规则（Feller, 1966）需要一个被叫做测度论（measure theory ）的数学分支，这超出的本书的范围。不过，它的正确性在直觉下是显然的。我们把实值变量分割为宽度为$\Delta$，然后考虑这些离散的区间上的概率分布。当$\Delta \to 0$时，把求和转换为积分就得到希望的结果了。