线性判别式的最简单形式是取输入向量的线性函数，即

$$y(x) = w^Tx + w_0 \tag{4.4}$$

其中$w$被称为权向量（weight vector），$w_0$是偏置（不要与统计中的偏置混淆）。偏置的相反数有时被称为阈值（threshold）。如果$y(x) \geq 0$则把输入向量$x$分到类$C_1$中，否则分到$C_2$中。因此，对应的决策边界由$y(x) = 0$确定，它对应着$D$维空间中的一个$(D-1)$维超平面。考虑两个点$x_A, x_B$都处在超平面上的情形。由于$y(x_A) = y(x_B) = 0$，得到$w^T(x_A - x_B) = 0$，所以向量$w$与在决策面上的所有向量都正交，因此$w$确定了决策面的方向。同样的，如果$x$在决策面，那么$y(x) = 0$，所以原点到决策面的标准距离由

$$\frac{w^Tx}{\Vert w \Vert} = -\frac{w_0}{\Vert w \Vert} \tag{4.5}$$

所以我们看到偏置参数$w_0$确定了决策面的位置。图4.1阐释了$D = 2$情况下的这些性质。

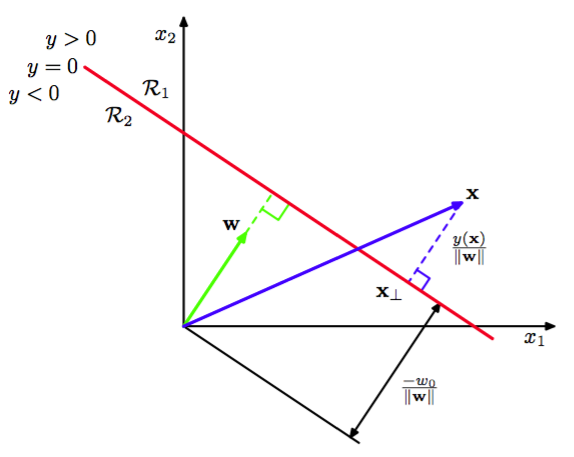
图 4.1 二维线性判别函数的几何表示

此外，我们注意到$y(x)$的值给出了点$x$到决策面的垂直距离$r$的一个有符号的度量。为了证明这点，考虑任意点$x$并令$x_{\perp}$是它在决策面上的正交投影，即

$$x = x_{\perp} + r\frac{w}{\Vert w \Vert} \tag{4.6}$$

两边同时乘以$w^T$并加上$w_0$，再利用$y(x)=w^Tx+w_0, y(x_{\perp})=w^Tx_{\perp} + w_0 = 0$得到

$$r = \frac{y(x)}{\Vert w \Vert} \tag{4.7}$$

图4.1阐释的这个结果。

与第3章线性回归模型相同，有时引入一个额外的虚“输入”$x_0 = 1$来使记号更简洁，会比较方便。然后定义$\tilde{w} = (w_0, w) \tilde{x} = (x_0, x)$，然后

$$y(x) = \tilde{w}^T\tilde{x} \tag{4.8}$$

在这种情况下，决策面是一个穿过$D+1$维扩展输入空间原点的$D$维超平面。