变分的方法起源于18世纪的欧拉、拉格朗日,以及其他的关于变分法(calculus of variations)的研究。标准的微积分关注的是寻找函数的导数。我们可以将函数想象为一个映射。这个映射以一个变量的值作为输入,返回函数值作为输出。函数的导数描述了当输入变量有一个无限小的变化时,输出值如何变化。类似地,我们可以将泛函(functional)作为一个映射,它以一个函数作为输入,返回泛函的值作为输出。一个例子是熵,它的输入是一个概率分布,返回下面的量
作为输出。我们可以引入泛函的导数(functional derivative)的概念,它表达了输入函数产生无穷小的改变时,泛函的值的变化情况(Feynman et al., 1964)。变分法的规则与标准的微积分规则很相似,在附录D中讨论。许多问题可以表示为最优化问题,其中需要最优化的量是一个泛函。研究所有可能的输入函数,找到最大化或者最小化泛函的函数就是问题的解。变分方法有很广泛的适用性,包括有限元方法(Kapur, 1989)和最大熵方法(Schwarz, 1988)。
虽然变分方法本质上没有任何近似的东西,但是它们通常会被用于寻找近似解。寻找近似解的过程可以这样完成:限制需要最优化算法搜索的函数的范围,例如只考虑二次函数,或考虑由固定的基函数线性组合而成的函数,其中只有线性组合的系数可以发生变化。在概率推断的应用中,限制条件的形式可以是可分解的假设(Jordan et al., 1999; Jaakkola, 2001)。
现在,让我们详细讨论变分最优化的概念如何应用于推断问题。假设我们有一个纯粹的贝叶斯模型,其中每个参数都有一个先验概率分布。这个模型也可以有潜在变量以及参数,我们会把所有潜在变量和参数组成的集合记作。类似的,我们会把所有观测变量的集合记作。例如,我们可能有个独立同分布的数据,其中且。我们的概率模型确定了联合概率分布,我们的目标是找到对后验概率分布以及模型证据的近似。与我们关于EM的讨论相同,我们可以将对数边缘概率分解,即
其中我们定义了
这与我们关于EM的讨论的唯一的区别是,因为参数现在是随机变量,被整合到了Z中,所以参数向量不再出现。由于本章中我们主要感兴趣的是连续变量,因此我们在这个分解的公式中使用了积分而不是求和。但是,如果某些变量或全部的变量都是离散变量,那么分析过程不变,只需根据需要把积分替换为求和即可。同样的,我们可以通过关于概率分布的最优化来使下界达到最大值,这等价于最小化KL散度。如果我们允许任意选择,那么下界的最大值出现在KL散度等于零的时刻,此时等于后验概率分布。然而,我们假定在需要处理的模型中,对真实的概率分布进行操作是不可行的。
于是,我们转而考虑概率分布的一个受限制的类别,然后寻找这个类别中使得KL散度达到最小值的概率分布。我们的目标是充分限制可以取得的概率分布的类别范围,使得这个范围中的所有概率分布都是可以处理的概率分布。同时,我们还要使得这个范围充分大、充分灵活,从而它能够提供对真实后验概率分布的一个足够好的近似。需要强调的是,施加限制条件的唯一目的是为了计算方便,并且在这个限制条件下,我们应该使用尽可能丰富的近似概率分布。特别的,对于高度灵活的概率分布来说,没有“过拟合”现象。使用灵活的近似仅仅使得我们更好地近似真实的后验概率分布。
限制近似概率分布的范围的一种方法是使用参数概率分布,它由参数集合控制。 这样,下界变成了的函数,我们可以利用标准的非线性最优化方法确定参数的最优值。图10.1给出了这种方法的一个例子,其中变分分布是一个高斯分布,并且我们已经关于均值和协方差进行了最优化。
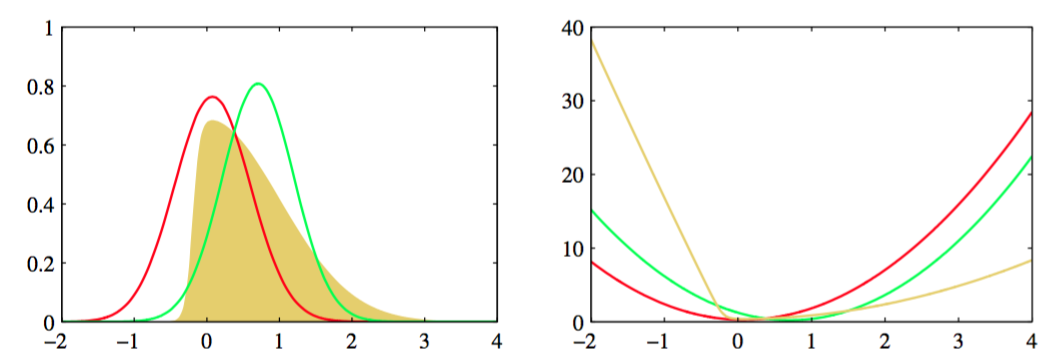
图 10.1 对于之前在图4.14中考虑过的例子进行变分近似的结果。左图给出了原始的概率分布(黄色)以及拉普拉斯近似(红色)和变分近似(绿色),右图给出了对应曲线的负对数。