在有向图的情形下,我们看到可以通过使用被称为D-划分的图检测方法判断一个特定的条件独立性质是否成立。这涉及到判断链接两个结点集合的路径是否被“阻隔”。然而,由于头到头 结点的存在,阻隔的定义多少有些微妙。我们可能会问,是否可以定义另一种概率分布的图语义表示,使得条件独立性由单一的图划分确定。这种情形确实存在,对应于无向图模型。通过移除图中链接的方向性,父结点和子结点的非对称性也被移除了,因此头到头结点的微妙性也 就不再存在了。
假设在一个无向图中,我们有三个结点集合,记作。我们考虑条件独立性质
为了判定由图定义的概率分布是否满足这个性质,我们考虑连接集合A的结点和集合B的结点的所有可能路径。如果所有这些路径都通过了集合中的一个或多个结点,那么所有这样的路径都被“阻隔”,因此条件独立性质成立。然而,如果存在至少一条未被阻隔的路径,那么性质条件独立的性质未必成立,或更精确地说,存在至少某些对应于图的概率分布不满足条件独立性质。图8.27给出了一个例子。
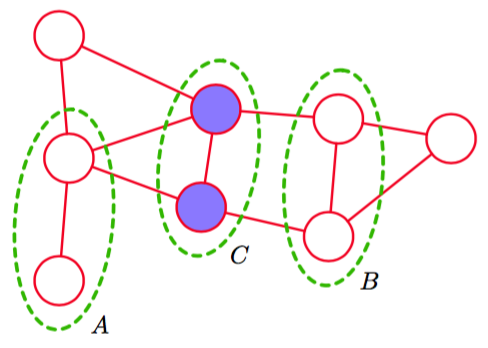
图 8.27 无向图的一个例子,其中从集合中的任意结点到集合中的任意结点的每天路径都通过集合中的至少一个结点。结果,对于所有由这个图描述的任意概率分布,以为条件,与都条件独立。
注意,这与D-划分的准则完全相同,唯一的差别在于没有头到头的现象。因此,无向图的条件独立性的检测比有向图简单。
另一种条件独立性的检测的方法是假设从图中把集合中的结点以及与这些结点相连的链接全部删除。然后,我们考察是否存在一条从中任意结点到中任意结点的路径。如果没有这样的路径,那么条件独立的性质一定成立。
无向图的马尔科夫毯的形式相当简单,因为结点只条件依赖于相邻结点,而条件独立于任何其他的结点,如图8.28所示。
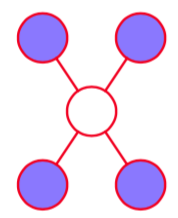
图 8.28 对于一个无向图,结点的马尔科夫毯由相邻结点的集合组成。它的性质为:以图中所有剩余变量为条件,的条件概率分布只依赖于马尔科夫毯中的变量。