现在，我们介绍多项式分布参数$\{\mu_k\}$的一组先验分布。观察多项式分布的公式，得到共轭先验：
$$p(\mu|\alpha) \propto \prod\limits_{k=1}^{K}\mu_k^{\alpha_k - 1}$$

其中$0 \leq \mu_k \leq 1 , \sum_k\mu_k = 1$，$(\alpha_1,...,\alpha_K)^T$记作$\alpha$是分布的参数。注意，由于总和的限制，$\{\mu_k\}$空间上的分布被限制在$K − 1$维的单纯形（simplex）中。图2.4展示了$K = 3$的情形。

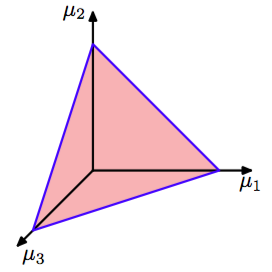
图 2.4 三个变量上的狄利克雷分布被限制在一个单纯形中

概率的标准形式为：

$$Dir(\mu|\alpha) = \frac{\Gamma(\alpha_0)}{\Gamma(\alpha_1)...\Gamma(\alpha_K)}\prod\limits_{k=1}^K\mu_k^{\alpha_k - 1} \tag{2.38}$$

这就是狄利克雷分布（Dirichlet distribution）。其中的$\Gamma(x)$是1.141中定义的gamma函数，

$$\alpha_0 = \sum\limits_{k=1}^K\alpha_k \tag{2.39}$$

图2.5展示的不同的参数$\alpha_k$的单纯形上的狄利克雷分布。

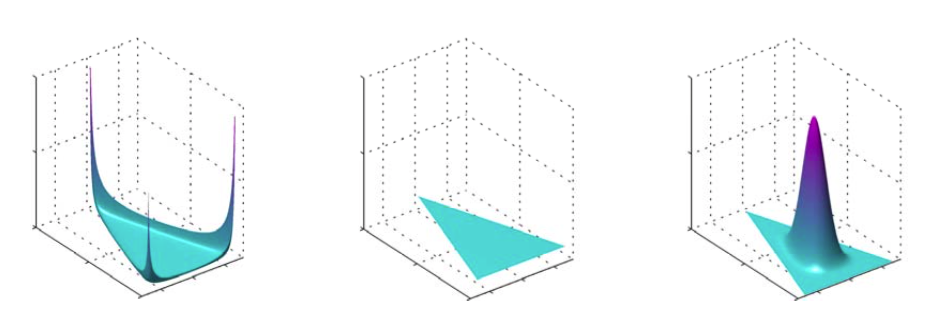
图 2.5 三个变量上的狄利克雷分布的图像，其中两个水平轴是单纯形平面上的坐标轴，垂直轴对应于概率密度的值。分布对应$\{\alpha_k\} = 0.1, \{\alpha_k\} = 1, \{\alpha_k\} = 10$。

公式（2.38）的先验乘以公式（2.34）的似然函数，得到参数$\{\mu_k\}$的后验分布公式：

$$p(\mu|D,\alpha) \propto p(D|\mu)p(\mu|\alpha) \propto \prod\limits_{k=1}^K\mu_k^{\alpha_k + m_k - 1} \tag{2.40}$$

我们看到后验分布还是狄利克雷分布，这说明，狄利克雷分布确实是多项式分布的共轭先验。这让我们能够通过与公式（2.38）比较，确定标准化参数。得到：

$$\begin{eqnarray} p(\mu|D, \alpha) &=& Dir(\mu|\alpha + m) \\ &=& \frac{\Gamma(\alpha_0 + N)}{\Gamma(\alpha_1+m_1)...+\Gamma(\alpha_K+m_K)}\prod\limits_{k=1}^K\mu_k^{\alpha_k + m_k - 1} \tag{2.41} \end{eqnarray}$$

其中$m = (m_1,...,m_K)^T$。与二项分布的beta先验一样，可以把狄利克雷分布参数$\alpha_k$当成观测到$x_k = 1$的数量。

注意，两个状态的量既可以用公式（2.9）的二项分布表示为二元变量，也可以用$K = 2$的公式（2.34）的多项式分布表示为“1-of-2”变量。