我们已经看到，对于由指数族分布描述的一大类的类条件分布，类别的后验概率是由特征变量的线性函数上的logistic（或softmax）变换给出的。然而，不是所有的类条件密度的后验概率都有这样简单的函数形式（例如，由高斯混合模型建模的类条件密度）。这表明研究其他类型的判别概率模型可能会很有价值。为了达到本章的目的，我们回到二分类的情形，再次使用一般的线性模型的框架，即

$$p(t=1|a) = f(a) \tag{4.111}$$

其中$a = w^T\phi$，且$f(\dot)$是激活函数。

选择其它链接函数的原因可以通过下面描述的噪声阈值模型得到。对于每个输入$\phi_n$，计算$a_n = w^T\phi_n$，然后根据

$$\begin{cases} t_n = 1 if a_n \geq \theta t_n = 0 otherwise \end{cases} \tag{4.112}$$

设置目标值。

如果$\theta$的值是从概率密度$p(\theta)$中取的，那么对应的激活函数是由累积分布函数

$$f(a) = \int_{-\infty}^a p(\theta)d\theta \tag{4.113}$$

给出，如图4.13所示

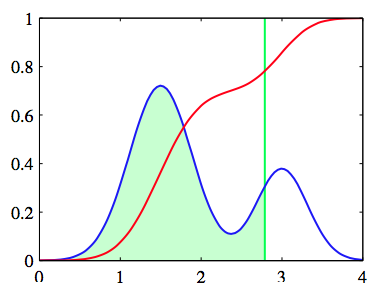
图 4.13 累积分布函数给出的激活函数

作为一个特殊的例子，假设密度$p(\theta)$是0均值，单位方差的高斯密度。对应的累计分布函数由

$$\Phi(a) = \int_{-\infty}^a\mathcal{N}(\theta|0,1)d\theta \tag{4.114}$$

给出，这就是我们所说的probit函数。 它具有sigmoid形状，并在图4.9中与logistic sigmoid函数做了对比。因为使用更一般的高斯分布等价于对线性系数$w$的缩放，所以它不会改变模型。很多数字计算包都提供与

$$erf(a) = \frac{2}{\sqrt{\pi}}\int_0^a exp(-\theta^2)d\theta \tag{4.115}$$

这个被称为erf函数或error函数（不要与机器学习模型中的误差函数相混淆）紧密相关的计算。它与probit函数的关系是

$$\Phi(a) = \frac{1}{2}\left\{1+\frac{1}{\sqrt{2}}erf(a)\right\} \tag{4.116}$$

基于probit激活函数的广义线性模型被称为probit回归。

我们可以直接推广之前讨论的思想，使用最大似然法来确定模型的参数。在实际应用中，使用probit回归得到的结果倾向于与logistic回归得到的结果类似。但是，当我们在4.5节讨论logistic回归的贝叶斯观点时，我们会找到probit模型的另一个应用。

在实际应用中经常出现的离群点的问题，它可能由输入向量$x$的测量误差，或目标值$t$的错误标记产生。由于这些点可以位于错误的一侧中距离理想决策边界相当远的位置上，因此他们会严重地干扰分类器。注意，在这一点上，由于当$x \to \infty$时logistice sigmoid函数会像$exp(−x)$那样渐进地衰减，而probit激活函数像$exp(−x^2)$那样衰减，因此probit模型对于离群点会更加敏感，logistic回归模型与probit回归模型的表现是不同的。

然而，logistic模型和probit模型都假设数据点被正确标记了。错误标记的影响可以很容易地合并到概率模型中。我们引入一个目标值$t$被标记为错误值的概率$\epsilon$(Opper and Winther, 2000a)。这时，数据点$x$的目标值的分布为

$$\begin{eqnarray} p(t|x) &=& (1-\epsilon)\delta(x) + \epsilon(1-\sigma(x)) \\ &=& \epsilon + (1-2\epsilon)\delta(x) \tag{4.117} \end{eqnarray}$$

其中$\delta(x)$是输入向量$x$的激活函数。这里，$\epsilon$可以实现设定，也可以被当成超参数，然后从数据中推断它的值。