边缘似然函数是通过对权重参数的积分来获得的,即:
计算这个积分的一种方法是再次使用式(2.115)给出的线性-高斯模型的条件分布的结果。这里,我们使用另一种通过对指数项配平方,然后使用高斯分布的标准化系数的基本形式,来计算这个积分。
从(3.11)(3.12)和(3.52)中,得到我们可以把证据函数写成
的形式。其中是的维数,且定义
如果忽略一些比例常数,式(3.79)可以看成与正则化的平方和误差函数相等。现在,对配平方,可得:
其中,我们引入了
和
注意对应的是误差函数的二阶导数矩阵
这被称为Hessian矩阵。这里我们定义为:
使用式(3.54),可得,因此式(3.84)等价于之前的定义的式(3.53),所以它表示后验分布的均值。
通过标准化多元高斯分布的标准化系数,就可以简单的得到关于的积分,即:
使用式(3.78)我们可以把对数边缘似然写成
这就是证据函数所需要的表达式。
回到多项式回归问题,我们可以画出模型证据与多项式阶数之间的关系,如图3.14所示。
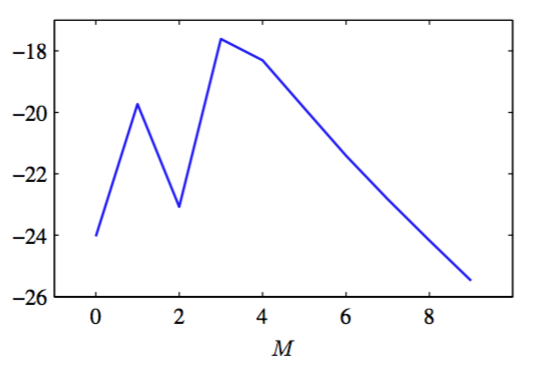
图 3.14 多项式回归模型的模型对数证据与阶数的关系图像
这里,我们已经假定先验分布的形式为式(1.65),参数的值固定为。这个图像的形式非常有指导意义。回头看图1.4,得到的多项式对数据的拟合效果非常差,结果模型证据的值也相对较小。的多项式对于数据的拟合效果有了显 著的提升,因此模型证据变大了。但是,对于的多项式,因为产生数据的正弦函数是奇函数,所以在多项式展开中没有偶次项,所以拟合效果又变差了。事实上,图1.5给出的数据残差从到只有微小的减小。由于复杂的模型有着更大的复杂度惩罚项,因此从到,模型证据实际上减小了。当时,我们对于数据的拟合效果有了很大的提升,如图1.4所示,因此模型证据再次增大,给出了多项式拟合的最高的模型证据。进一步增加的值,只能少量地提升拟合的效果,但是模型的复杂度却越来越复杂,这导致整体的模型证据下降。再次看图1.5,我们看到泛化错误在到之间几乎为常数,因此只基于这幅图很难对模型做出选择。然而,模型证据的值明显地倾向于选择的模型,因为这是能很好地解释观测数据的最简单的模型。