假设我们的目标是简单的尽可能的少做出错误的分类。我们需要一个规则把每个$x$分到一个可用的分类中，这样的规则把输入空间切分成区域$R_k$，称为决策区域（decision regions）。每个类别对应一个决策区域，如$R_k$中所有点都被分为类$C_k$。决策区域间的边界被称为决策边界（decision boundaries）或决策面（decision surfaces）。注意一个决策区域不一定要连续的，可以由几个分离的区域组成。后续的章节中，我们会给出决策边 界和决策区域的例子。为了找到最优的决策规则，先考虑只有两种类别的情况，就像癌症问题一样。错误发生在把属于$C_1$的分到了$C_2$中，反之亦然。发生这种情况的概率为：

$$\begin{eqnarray} p(mistake) &=& p(x \in R_1, C_2) + p(x \in R_2, C_1) \\ &=& \int_{R_1} p(x, C_2)dx + \int_{R_2} p(x, C_1)dx \tag{1.78} \end{eqnarray}$$

可以随意选择把点$x$分到两类中的一类的决策规则。很明显为了最小化$p(mistake)$对于$x$的分类结果应该让公式（1.78）中被积函数尽可能的小。因此，对于$x$如果$p(x, C_1) > p(x, C_2)$，那么就把$x$分到类$C_1$中。根据乘积规则得到$p(x, C_k) = p(C_k|x)p(x)$。由于两项的因子$p(x)$是相同的，所以可以重新定义结果：最小化错误分类的概率可以通过把$x$分到使后验概率$p(C_k|x)$最大的分类中。图1.24展示了一元输入变量$x$的二元分类问题

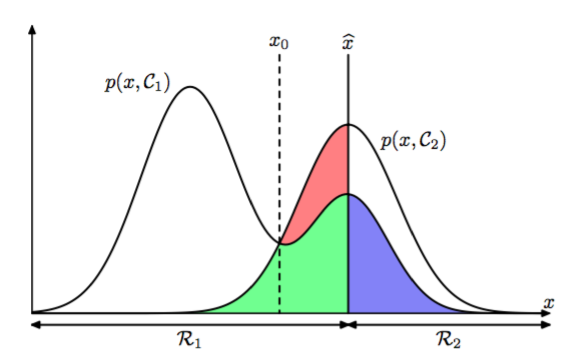
图 1.24: 两个类别的联合概率分布$p(x,C_k)$与$x$的关系，以及决策边界$x = \hat{x}$。$x \geq \hat{x}$的值被分类为$C_2$，因此属于决策区域$R_2$，而$x < \hat{x}$的值被分类为$C_1$，属于区域$R_1$。错误出现在蓝色、绿色和红色区域，从而对于$x < \hat{x}$，错误的来源是将属于类别$C_2$的点错分到类别$C_1$（表示为红色区域与绿色区域的总和），同样的，对于$x \geq \hat{x}$的点，错误的来源是将属于类别$C_1$的点错分到类别$C_2$（表示为蓝色区域）。当我们改变决策区域的位置$\hat{x}$时，绿色区域和蓝色区域的总面积是一个常数，而红色区域的面积发生改变。$\hat{x}$的最优选择是$p(x, C_1)$的曲线与$p(x, C_2)$的曲线相交，对应于$\hat{x} = x_0$，因为此时红色区域消失。这等价于最小化错误分类率的决策规则，这个规则将$x$分配到具有最大的后验概率$p(C_k|x)$的区域中。

对于更一般的$K$类的情形，最大化正确率会稍微简单一些，即最大化：

$$\begin{eqnarray} p(correct) &=& \sum\limits_{k=1}^K p(x \in R_k, C_k) \\ &=& \sum\limits_{k=1}^K\int_{R_k}p(x, C_k)dx \tag{1.79} \end{eqnarray}$$

当区域$R_k$的选择使得每个$x$的分类得到的$p(x, C_k)$最大时，上式取到最大值。再一次使用乘法规则$p(x, C_k) = p(C_k | x)p(x)$，并且因子$p(x)$对于所有项都相同，可以得到每个$x$都应该被分到有最大后验概率$p(C_k|x)$的类别中。