我们通过考虑离线手写数字数据集来说明PCA对于数据压缩的应用,其中我们关注与数字“3”的图像。由于协方差矩阵的每个特征向量是原始D维空间的一个向量,因此我们可以将特征向量表示为与数据点具有相同大小的图像。图12.3给出了前四个特征向量以及对应的特征值。
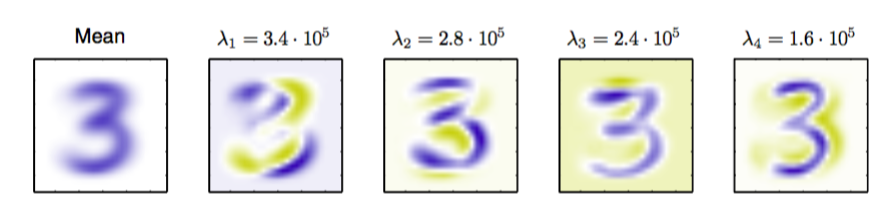
图 12.3 对于离线手写数字数据集中的数字“3”,图中给出了均值向量以及前四个PCA特征向量还有对应的特征值。蓝色对应于正值,白色对应于0,黄色对应于负值。
完整的特征值的图像,按照降序排序,如图12.4(a)所示。
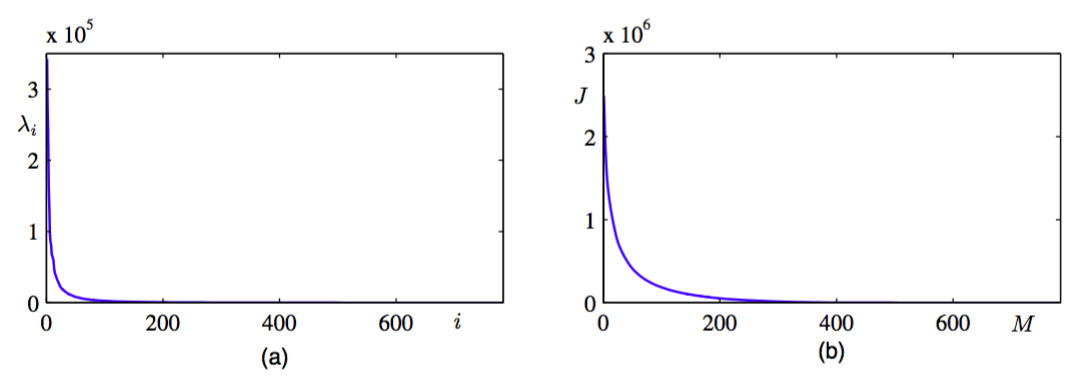
图 12.4 (a)对于离线手写数字数据集里的数字“3”的特征值谱线。(b)丢弃的特征值的加和的图像,它表示将数据投影到维主成分子空间中引入的平方和失真。
选择的一个特定的值造成的失真度量由到的特征值的求和给出。对于不同的值,图像如图12.4(b)所示。
如果我们将式(12.12)和(12.13)代入(12.10),我们可以写出对数据向量的PCA近似,形式为
其中我们使用了关系
这个关系来自于的完整性。这种方法表示了对数据集的一个压缩,因为对于每个数据点,我们将维向量替换为维向量,元素为。的值越小,压缩的程度越大。对于手写数字数据集里的数字“3”的数据点,使用PCA重建的例子如图12.5所示。
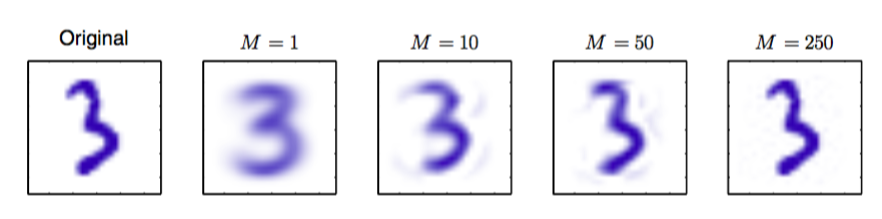
图 12.5 来自离线手写数字数据集的原始样本,以及对于不同的值,保留M个主成分得到的PCA重建。 随着的增加,重建变得越来越精确。当时,会得到一个完美的重建。
主成分分析的另一个应用是数据预处理。在这种情况下,目标不是维度降低,而是对数据集进行变换,使得数据集的某些属性得到标准化。这对于后续将模式识别算法成功应用于数据集来说很重要。通常,当原始变量使用不同的单位进行测量,或者变化情况相当不同的时候,我们会对数据集进行这样的变换。例如,在忠老泉数据集里,两次喷发的间隔时间通常要比喷发的持续时间大若干个数量级。当我们将K均值算法应用于这个数据集时,我们首先对各个变量进行单独的重新标度,使得每个变量的均值为0,方差为单位方差。这被称为对数据的标准化(standardize),并且标准化的数据的协方差矩阵的元素为
其中是的标准差。这被称为原始数据集的相关性矩阵(correlation matrix),具有下面的性质:如果数据的两个分量和完全相关,那么,如果它们不相关,那么。
然而,使用PCA,我们可以对数据进行更显著的标准化,得到零均值和单位方差的数据,从而不同的变量之间的相关性关系被消除。为了完成这一点,我们首先将特征向量方程(12.17)写成下面的形式
其中,是一个的对角矩阵,元素为,是一个的正交矩阵,列为。然后对于每个数据点,我们定义一个变换,值为
其中是式(12.1)定义的样本均值。很明显,集合的均值为0 ,协方差是单位矩阵 ,因为
这个操作被称为对数据的白化(whitening)或球形化(sphereing)。图12.6使用忠老泉数据说明了这一点。
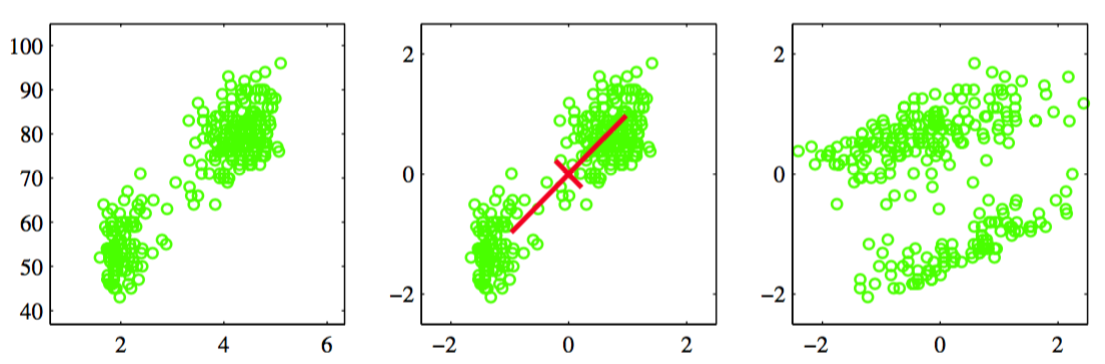
图 12.6 对忠老泉数据集进行线性预处理的效果。左图给出的原始的数据。中图给出了将各个变量标准化为零均值单位方差的结果。同时画出的还有这个归一化数据集的主轴,画出了的范围。右图给出了对数据进行白化的结果,得到了零均值单位协方差的数据。
将PCA与4.1.4节讨论的Fisher线性判别分析进行对比是很有趣的。两种方法都可以看成线性维度降低的例子。然而,PCA是无监督的,值依赖于的值,而Fisher线性判别分析还使用了 类别标签的信息。图12.7给出的例子强调了这个区别。
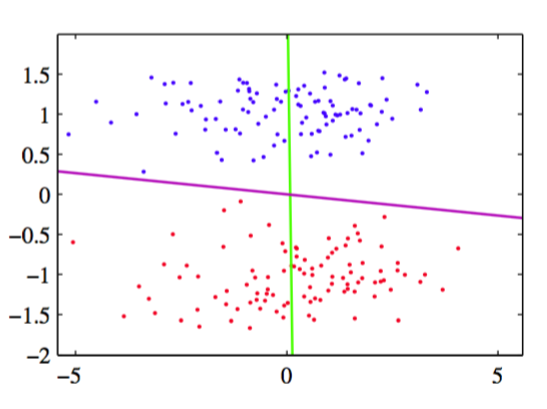
图 12.7 用于线性维度降低的主成分分析与Fisher线性判别分析的对比。这里,数据位于二维空间中,属于两个类别,用红色和蓝色表示。数据要被投影到一维空间中。PCA选择了最大方差的方向,由紫色直线表示,它产生了严重的类别覆盖。而Fisher线性判别分析考虑类别标签,产生了在绿色直线上的投影。 这种投影对类别的区分效果要好得多。
主成分分析的另一个常见应用是数据可视化。这里,每个数据点被投影到二维的主子空间中,从而数据点被画在了一个笛卡尔坐标系中,坐标系由和定义,其中和是特征向量,对应于最大的和第二大的特征值。对于石油流数据集,这种图的一个例 子如图12.8所示。
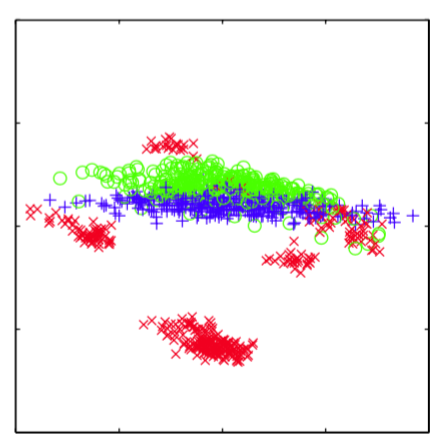
图 12.8 石油流数据的可视化,通过将数据投影到前两个主成分上的方式实现。红色、蓝色和绿色点分别对应“薄片状”、“同质状”和“环状”的石油流配置。