我们以介绍模型参数的先验概率分布来开始我们的线性回归的贝叶斯方法讨论。这个阶段,我们把噪声精度参数当做已知常数。首先,注意到,式(3.10)定义的似然函数是的二次函数的指数形式。于是对应的共轭先验是形式为
均值和方差分别为的高斯分布。
接下来,计算后验分布,它是正比于似然函数与先验的乘积。因为选择共轭高斯先验分布,所以后验同样是高斯。可以对指数项进行配平方,然后通过标准高斯的标准结果来找到标准化系数,来估计这个分布。由于在推导公式(2.116)时,已经进行了必要的工作,所以我们能够直接写出后验概率分布的形式:
其中
注意,由于后验分布是高斯的,它的众数与均值正好相同。因此最大后验权向量由给出。如果考虑一个无限宽的先验,其中,那么后验分布的均值就退化成了由式(3.15)给出的最大似然值。类似地,如果,那么后验分布就被还原成先验分布。此外,如果数据点是顺序到达的,那么任何一个阶段的后验分布都可以看成后续数据点的先验分布。此时新的后验分布再次由式(3.49)给出。
为了简化起见,本章的剩余部分,我们介绍一个特定的形式高斯先验。具体来说,是一个只由一个精度参数控制的零均值各向同性高斯分布:
且对应的关于的后验分布由式(3.49)给出,其中
后验分布的对数是由对数似然与先验的对数的和给出的一个关于的函数,形式为:
关于来最大化这个后验分布等价于最小化加上一个二次正则项的平方和误差函数,正则项对应的式(3.27)。
我们可以使用简单的直线拟合的例子来阐述线性基函数的贝叶斯学习过程,以及后验分布的顺序更新过程。考虑单输入变量,单目标变量和线性模型形式。因为它只有两个可调节参数,所以我们可以直接在参数空间中画出先验或后验分布。我们从带有参数的函数中生成数据。生成方法是:首先从均匀分布中选择的值,再计算,最后加上一个标准差为0.2的高斯噪声,得到目标变量。我们的目标是从这样的数据中恢复的值,并探索模型对数据集规模的依赖关系。这里我们假设噪声方差是已知的,所以我们把精度参数设置为它的真实值。同样的,我们把固定为。我们稍后会简短地讨论从训练数据中确定的策略。图3.7展示了当数据集的规模增加时贝叶斯学习的结果,还展示了贝叶斯学习的顺序本质,即当新数据点被观测到的时候,当前的后验分布变成了先验分布。
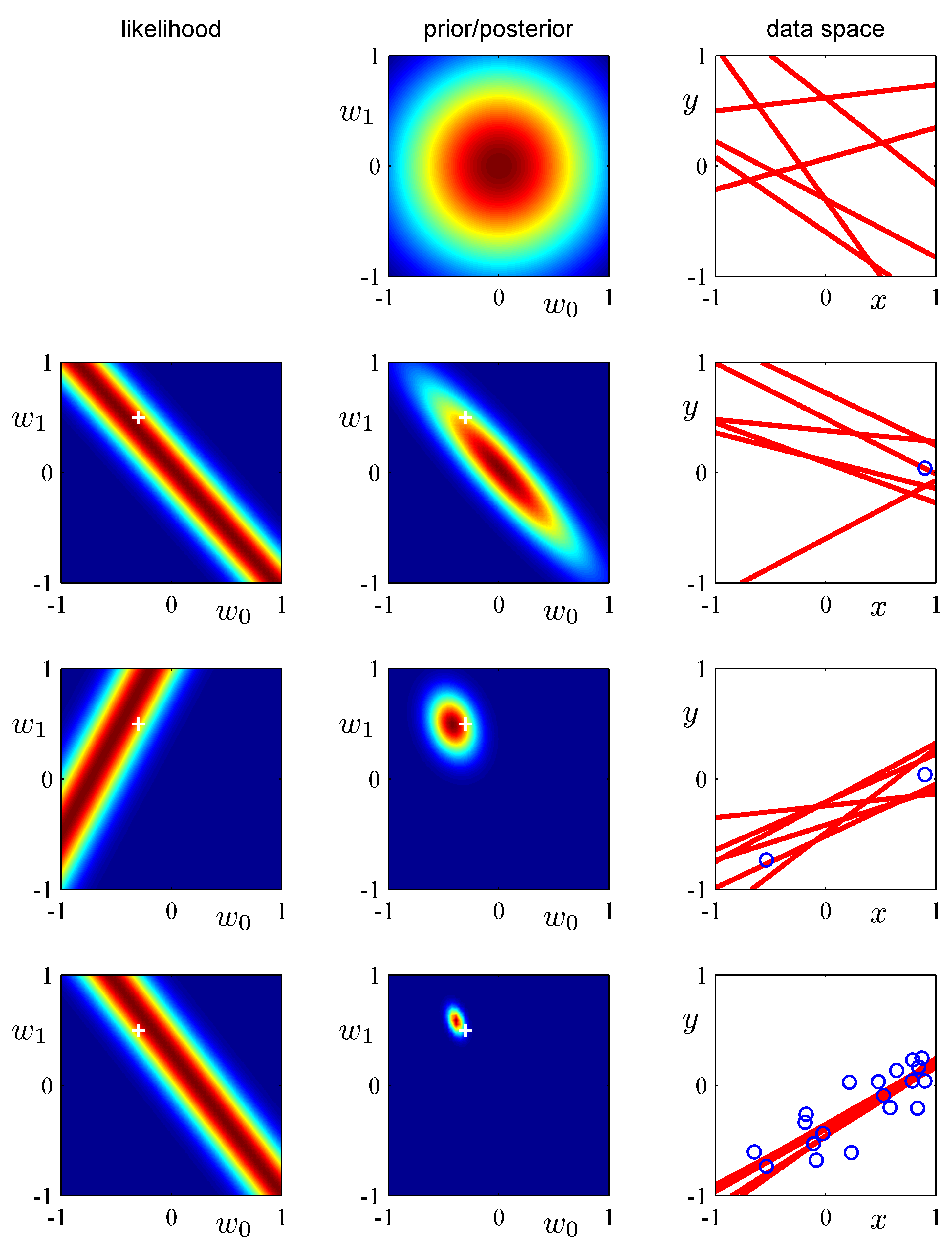
图 3.7 顺序贝叶斯学习
花时间仔细研究一下这幅图是很值得的,因为它说明了贝叶斯推断的一些重要的概念。这幅图的第一行对应着,观测到数据之前,空间中先验分布的图像,以及六个从先验中获得的函数。第二行展示了观测到一个数据点之后的情形。数据点的位置由右手边的列中的蓝色圆圈表示。左手边的列展示了这个数据点的似然函数关于的函数图像。注意,似然函数给出了直线必须穿过数据点附近的位置的软性限制,其中附近由噪声精度确定。为了进行对比,用来生成数据集的真实参数值在图3.7的右手边的列以白色十字标记出来。我们用这个似然函数乘以从最上面一行得到的先验,然后标准化后得到的后验分布展示在第二行的中间。从这个后验分布得到的的样本对应的回归函数展示在右手边。注意,这些直线样本都穿过数据点的附近。这幅图的第三行展示了观测到第二个点的效果,同样以蓝色圈展示在右手边的列中。对应这个数据点自身的似然函数展示在左边图像中。如果我们把这个似然函数与第二行的后验概率分布相乘,就得到了第三行中间一列的图展示的后验分布。注意,这个后验分布与我们将原始的先验分布结合两个数据点的似然函数得到的后验概率分布完全相同。现在,后验概率分布被两个数据点影响。由于两个点足够定义一条直线,因此已经得到了相对紧凑的后验分布。这个后验分布中的样本给出了第三列中红色的函数图像。我们看到这些函数同时穿过了两个数据点的附近。第四行展示了观测到全部20个数据点的效果。左侧的图展示了第20个数据点自身的似然函数,中间的图展示了吸收了全部20个测试信息所给出的后验分布。注意,这个后验比第三行的变得更加尖锐。在无穷多数据点的极限情况下,后验概率分布会变成一个以真实参数值(以白色十字标记)为中心的Delta函数。
其他形式的参数先验也可以被考虑。例如,我们可以推广高斯先验分布,得到:
当时对应着高斯分布,并且只有在这种情形下的先验才与式(3.10)给出的似然函数共轭。找到的后验概率分布的最大值等价于找到正则化误差函数(3.29)的最小值。在高斯先验的情况下,后验概率分布的众数等于均值,但是当时这个性质就不成立了。