高斯也称为正态分布,是连续变量分布上广泛使用的一种模型。对于单变量,高斯分布可以写成:
其中分别为均值和方差。对于维向量,多变量的高斯分布形式为:
其中为维均值向量,为的协方差矩阵。是的行列式。
高斯分布会出现在许多不同的问题中,可以从多个不同的角度来理解。例如,我们已经证明,对于单个实值变量,使熵最大的是高斯分布。这个性质同样适用于多变量高斯。
另一种情况是,多个随机变量之和也会产生高斯分布。中心极限定理(由拉普拉斯提出)告诉我们,温和的一组随机变量的和的概率分布随着项的增加,趋向于高斯分布(Walker, 1969)。为了阐述这个,考虑个区间[0, 1]上的均匀分布的随机变量,确定它们的均值的分布。如图2.6展示的,对于大的,趋向于高斯分布。
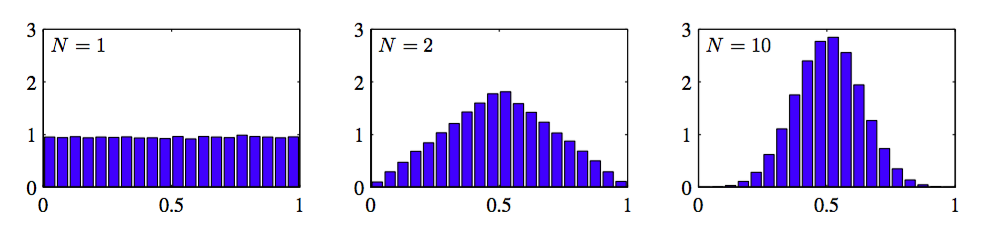
图 2.6 均匀分布的和的均值的直方图
在实际应用中,随着N的增加,分布会很快的收敛于高斯分布。由这个结论可得:式(2.9)定义的二元随机变量在次观测中出现次的二项分布将会在时趋向于高斯分布(图2.1给出了的情形)。
现在详细讨论高斯分布中的一些重要的分析性质。这就使得这节内容依赖于之前所介绍的技术,并且需要对各种矩阵性质比较熟悉。我们强烈鼓励读者能够使用这里介绍的技术熟练操作高斯分布,因为这对于理解后续章节中出现的更加复杂的模型非常有帮助。
首先,考虑高斯分布的几何形式。高斯通过出现在指数位置上的
这个二次型依赖于。被称为到的马氏距离( Mahalanobis distance),当是单位矩阵时,退化成欧式距离。当这个二次型在空间中是常数的时候,高斯分布的曲面也是常数。
首先,我们注意到矩阵可以不失一般性的取为对称矩阵,因为任何非对称项都会从指数中消失。现在考虑,协方差矩阵的特征向量方程:
其中。因为是实对称矩阵,所以它的特征值也是实数,特征向量可以从正交集中选择,得到:
其中是单位矩阵的第个元素,满足:
协方差矩阵可以表示成特征向量的展开的形式:
同样的协方差的逆矩阵可以表示为
公式(2.49)代入(2.44),可以把二次型表示为:
其中
我们可以把解释为由正交向量关于原来的坐标系平移和旋转之后得到的新坐标系。记,可得:
其中是由行向量组成的。根据公式(2.46)可得是正交矩阵,即它满足,其中是单位矩阵。
如果公式(2.50)是常数时,那么二次型和高斯密度在曲面上为常数。如果所有特征值都是正的,那么这些曲面是中心位于,轴方向为,轴方向的缩放比例为的椭球面,如图2.7所示。
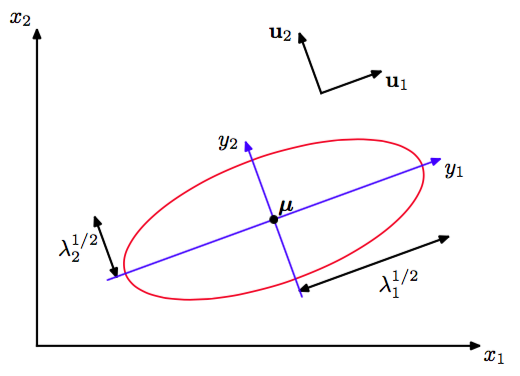
图 2.7 椭球面
为了很好的定义高斯分布,需要协方差矩阵的特征值严格为正,不然分布就不能标准化。每一个特征值都严格为正的矩阵被称为正定的(positive definite)。在12章中,我们会遇到一个或者多个特征值为零的高斯分布,那种情况下分布是奇异的,被限制在低维的子空间中。每一个特征值都非负的矩阵被称为半正定的(positive semidefinite)。
现在,在由定义的新坐标系中,高斯分布的形式。从坐标系转换到坐标系的Jacobian矩阵为:
其中是矩阵的元素。有矩阵的正交性,可得Jacobian矩阵的行列式的平方为:
由此可得。且协方差矩阵的行列式可以写成特征值的乘积:
因此,在坐标系下,高斯分布由以下形式:
这是个独立的一元高斯分布的乘积。特征向量定义了一系列平移,旋转变换,使联合概率分布转行为独立分布的乘积。分布关于坐标系的积分为:
其中使用了公式(1.48)的结果来标准化一元高斯分布。多元高斯分布公式(2.43)必然是标准化的。
现在,我们考察高斯分布的动差,并提供参数的解释。高斯分布的的期望是:
其中使用了替换了变量。注意,指数函数是关于的偶函数,且积分范围是,根据对称性项中的可以消去。因此:
所以是高斯分布的均值。
现在,考虑高斯分布的二阶动差。在一元的情况下,二阶动差由给出。对于多元高斯分布,有个二阶动差,由给出,组合在一起得到矩阵。这个矩阵可以写成:
再一次使用了替换了变量。注意,交叉项由对称性再一次消去。项是不变的,可以提取出来放到积分的外面。因为高斯分布是标准化的,所以它自己是等于单位矩阵。考虑涉及的项。可以再次使用公式(2.45)给出的协方差矩阵的特征向量展开,和特征向量的完备性,得到:
其中,推出:
其中使用了特征向量方程(2.45),以及中间一行右侧的积分除了其他可以由对称性消去。最后一行使用了公式(1.50),(2.55)的结果和公式(2.48)一起,得到:
对于单个随机变量,为了定义方差,在计算二阶动差时,要先减去均值。同样的,对于多元变量,减掉均值同样很方便。这就得到了随机向量的协方差:
对于高斯分布的特殊情况,我们可以使和公式(2.62)的结果一起,得到:
由于参数矩阵控制了高斯分布下的协方差,所以把它叫做协方差矩阵。
尽管,高斯分布(2.43)被当作密度模型广泛使用,但是它有着一些巨大的局限性。考虑分布中自由参数的数量。一个通用的对称协方差矩阵有个独立参数,和中的另外个独立参数,总共个参数。对于大的,参数的总数以的平方的方式增长,且大矩阵的计算和求逆会相当困难。解决这个问题的一种方式是使用限制形式的协方差矩阵。如果考虑对角化的协方差矩阵,即,那么密度模型中总共有个独立参数。对应的常数密度的轮廓线由轴对齐的椭球给出。可以进一步地限制协方差矩阵为单位矩阵的倍数,即(这被称为同性协方差),那么模型总共有个独立参数,且得到恒定密度的球面。图2.8分别展示了通用的、对角的以及同性的协方差矩阵的概率。
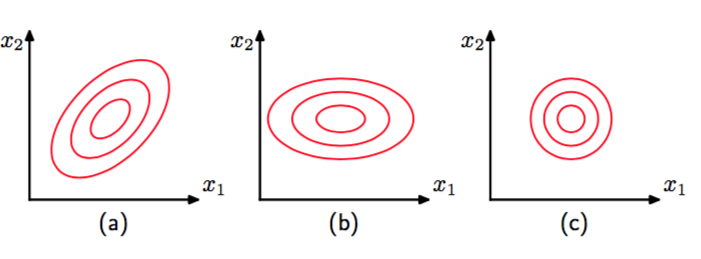
图 2.8: 二维高斯分布的固定概率密度等高线。其中,(a)图对应的协方差矩阵为一般形式,(b)图对应的协方差矩阵为对角矩阵,图中椭圆的等高线与坐标轴对齐,(c)图对应的协方差矩阵正比于单位矩阵,图中的等高线是同心圆。
不幸的是,尽管这样的方法限制了概率分布的的自由度的数量,使得求协方差矩阵的逆可以很快地完成,但也极大地束缚了概率密度的形式,且限制了它获取数据中有趣的相关性的能力。
高斯分布的另一个局限是它本质上是单峰的(即只有一个最大值),因此不能够很好地近似多峰分布。因此高斯分布一方面相当灵活,因为它有很多参数。另一方面,它又有很大的局限性,因为它不能够描述很多概率分布。稍后我们介绍的潜变量(latent variables),也被称为隐藏变量(hidden variable)或者未观测变量(unobserved variable),可以解决这两个问题。特别的,通过引入离散的潜变量,相当多的多峰分布可以使用混合高斯分布来描述,就像2.3.9节描述的那样。同样的,12章中介绍的连续潜变量,可以使模型的自由参数的数量可以控制成与维数据空间无关。同时又能描述数集里主要的相关性。实际上,这两种方法可以结合起来,进一步扩展,可以推导出一大类适用于相当多的实际应用层次模型。例如,在图像的概率模型中广泛使用的马尔科夫随机场(Markov random field)的高斯版本,是像素灰度的联合空间上的高斯分布,但是通过引入能够反映空间中像素组织的结构,可以很方便地处理。同样的,对时间序列数据的应用(例如跟踪)进行建模的线性动态系统(linear dynamical system),是涉及到相当多的观测变量和潜变量的联合高斯分布,同样可以通过分布上的结构信息很方便的处理。概率图模型,表达这种复杂分布的形式和性质的一个强大的框架。将是第8章的主题。
一些证明
2.48, 2.49
我们可以把式(2.48)的右手边写成矩阵形式:
其中是一个以特征向量为列的的矩阵,是对角线上的值为的对角矩阵。 因此,我们就有
同时,根据式(2.45)-(2.47)我们有
因此,得到 即(2.48)成立。
此外,由于是正交的,所以。然后我们就有