首先,我们考虑一个二元随机变量。例如,可能描述了扔硬币的结果,表示“正面”,表示反面。我们可以假设由一个损坏的硬币,这枚硬币正面朝上的概率未必等于反面朝上的概率。的概率被记作参数:
其中,那么就得到。的概率分布就可以写成:
这叫做伯努利分布(Bernoulli distribution)。很容易验证这个分布是标准化的,它的均值和方差:
现在假设的观察数据集。假设观测值是独立的从中抽取,那么就可以构造关于的似然函数:
在频率学的观点中,可以通过最大化似然函数来估计的值,或等价的,最大化对数似然函数。在伯努利分布的情形下,对数似然函数为:
值得一提的是对数似然函数只通过依赖于次观测值。这个和式是这个分布下数据的充分统计量(sufficient statistic),我们后面将详细研究充分统计量的重要作用。对关于微分并使它等于0,我们就得到最大似然估计:
也被称为样本均值(sample mean)。如果我们把数据集里(正面朝上)的观测的数量记作,那么我们可以把公式(2.7)写成下面的形式:
在最大似然的框架中,数据集中正面朝上的比列就是它的的概率。
现在,我们抛3次硬币,并观测到3次都是正面朝上,那么就有 。在这个例子中,最大似然会预测将来所有的观测都是正面朝上。常识告诉我们这是不合理的。事实上,这是最大似然过拟的一个极端例子。稍后会看到,通过引入的先验分布,我们会得到一个更合理的结论。
我们可以计算出数据集大小为的具有个的观测值的概率分布。这被称为二项式分布(binomial distribution),根据公式(2.5)得到它正比于。为了得到标准化的系数,在次抛硬币的过程中,需要把所有出现正面的次数加起来得到,所以二项式分布可以写成:
其中
表示从个相同的物体中选出个的方式的次数。图2.1展示了当时的二项式分布。
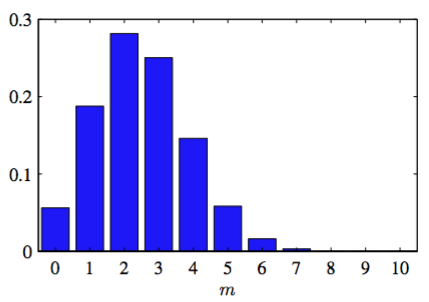
图 2.1 二项式分布
二项式分布的均值和方差可以从练习1.10的结果:独立事件的和的均值等于均值的和、和的方差等于方差的和来获得。根据,且对于由公式(2.3)(2.4)给出的每个观测值的均值和方差,我们得到:
这些结果可以直接通过微积分(离散型为求和)来证明。