现在，考虑最小二乘方法的几何解释比较有指导意义。为了达到这个目的，考虑坐标轴由$t_n$给出的$N$维空间，$\textbf{t} = (t_1,...,t_N)^T$是空间中的向量。通过$N$个点估计出的每个基函数$\phi_j(x_n)$也可以表示成相同空间中的一个向量，记作$\varphi_j$，如图3.2展示。

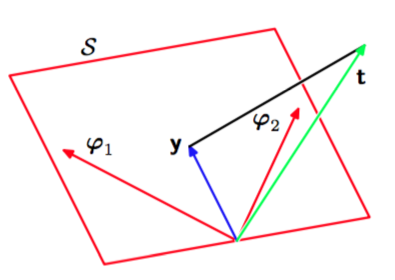
图 3.2 最小二乘几何解释

注意$\varphi_j$对应的是$\Phi$的第$j$列，而$\phi(x_n）$对应的是$\Phi$的第$n$行。如果基函数的数量$M$小于数据点的数量$N$，那么$M$个向量$\phi_j(x_n)$可以生成$M$维线性子空间$S$。我们定义$\textbf{y}$是$N$维向量，其中第$n^{th}$个元素由$y(x_n,w) , n = 1,....,N$。由于$\textbf{y}$是向量$\varphi_j$的任意线性组合，所以它可以在$M$维子空间的任意位置。平方和误差（3.12）等于$\textbf{y, t}$之间的欧式距离（相差一个因子1/2）。所以$w$的最小二乘解，对应子空间$S$中与$t$最近的$\textbf{y}$的选择。直观地来说，从图3.2得到，我们预期这个解与$t$在子空间$S$上的投影正交。我们看到$\textbf{y}$的解是由$\Phi w_{ML}$给出的，然后可以很容易的证明它就是是正交投影的形式这一事实。

在实际应用中，当$\Phi^T\Phi$接近奇异矩阵时，直接求解标准方程会导致数值计算上的困难。特别地，当两个或更多的基向量$\varphi_j$共线或接近共线时，参数的结果会相当大。这样的退化在处理真实数据集的时候并不少见。这样的数值计算上的困难可以通过奇异值分解（singular value decomposition）简称SVD的方法来解决（Press et al., 1992; Bishop and Nabney, 2008）。注意，额外的正则项可以确保即使在退化的情况下，矩阵也是非奇异的。