首先，我们考虑如何从简单的非均匀分布中生成随机数，假定我们已经有了一个均匀分布的随机数的来源。假设$z$在区间$(0, 1)$上均匀分布，我们使用某个函数$f(\dot)$对$z$的值进行变换，即$y = f(z)$。$y$上的概率分布为

$$p(y) = p(z)\left|\frac{dz}{dy}\right| \tag{11.5}$$

其中，在这种情况下，$p(z) = 1$。我们的目标是选择一个函数$f(z)$使得产生出的$y$值具有某种所需的具体的分布形式$p(y)$，对式（11.5）进行积分，我们有

$$z = h(y) \equiv \int_{-\infty}^y p(\hat{y})d\hat{y} \tag{11.6}$$

它是$p(y)$的不定积分。因此，$y = h^{−1}(z)$，因此我们必须使用一个函数来对这个均匀分布的随机数进行变换，这个函数是所求的概率分布的不定积分的反函数，如图11.2所示。

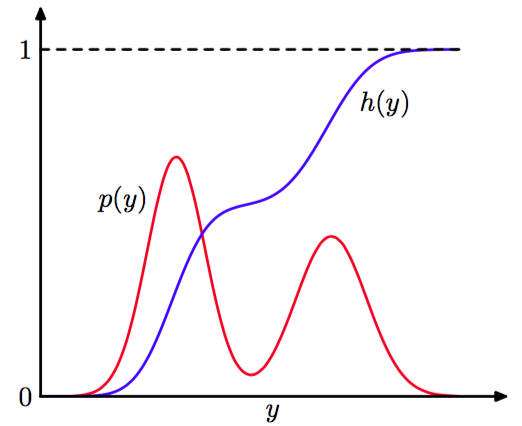
图 11.2 生成非均匀分布的随机数的变换方法的几何表示。$h(y)$是所求概率分布$p(y)$的不定积分。如果一个均匀分布的随机变量$z$使用$y = h^{−1}(z)$进行变换，那么$y$会服从概率分布$p(y)$。

考虑指数分布（exponential distribution）

$$p(y) = \lambda exp(-\lambda y) \tag{11.7}$$

其中$0 \leq y < \infty$。在这种情况下，式（11.6）的积分下界为0，因此$h(y) = 1 − exp(−\lambda y)$。从而，如果我们将均匀分布的变量$z$使用$y = −\lambda^{−1} \ln(1 − z)$进行变换，那么$y$就会服从指数分布。

另一种可以应用变换方法的概率分布是柯西分布

$$p(y) = \frac{1}{\pi}\frac{1}{1 + y^2} \tag{11.8}$$

这种情况下，不定积分的反函数可以用$\tan$函数表示。

对于多个变量情形的推广是很容易的，涉及到变量变化的Jacobian行列式，即

$$p(y_1,...,y_M) = p(z_1,...,z_M)\left|\frac{\partial(z_1,...,z_M)}{\partial(y_1,...,y_M)}\right| \tag{11.9}$$

作为变换方法的最后一个例子，我们考虑Box-Muller方法,用于生成高斯概率分布的样本。首先，假设我们生成一对均匀分布的随机变量$z_1,z_2 \in (−1,1)$，我们可以这样生成：对$(0,1)$上的均匀分布的变量使用$z \to 2z − 1$的方式进行变换。接下来，我们丢弃那些不满足$z_1^2 + z_2^2 \leq 1$的点对。这产生出单位圆内部的一个均匀分布，且$p(z_1, z_2) = 1 / pi$，如图11.3所示。

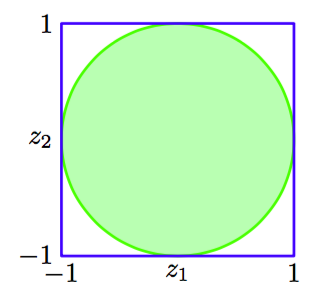
图 11.3 Box-Muller方法用于生成高斯分布的随机数，方法在开始时使用的是单位圆内部均匀分布的样本。

然后，对于每对$z_1, z _2$，我们计算

$$\begin{eqnarray} y_1 &=& z_1\left(\frac{-2\ln r^2}{r^2}\right)^{1/2} \tag{11.10} \\ y_2 &=& z_2\left(\frac{-2\ln r^2}{r^2}\right)^{1/2} \tag{11.11} \end{eqnarray}$$

其中$r^2 = z_1^2 + z_2^2$。这样，$y_1, y_2$的联合概率分布为

$$\begin{eqnarray} p(y_1,y_2) &=& p(z_1,z_2)\left|\frac{\partial(z_1,z_2)}{\partial(y_1,y_2)}\right| \\ &=& \left[\frac{1}{\sqrt{2\pi}}exp\left(\frac{-y_1^2}{2}\right)\right]\left[\frac{1}{\sqrt{2\pi}}exp\left(\frac{-y_2^2}{2}\right)\right] \tag{11.12} \end{eqnarray}$$

因此$y_1, y_2$是独立的，且每个都服从高斯分布，均值为0，方差为1。

如果$y$服从高斯分布，且均值为0，方差为1，那么$\sigma y + \mu$也服从高斯分布，均值为$\mu$，方差为$\sigma^2$。为了生成向量值的变量，且这个变量服从多元高斯分布，均值为$\mu$，协方差为$\Sigma$，我们可以使用Cholesky分解，它的形式为$\Sigma = LL^T$（Press et al., 1992）。这样，如果$z$是一个向量值的随机变量，且它的元素是独立的，并且服从均值为0、方差为1的高斯分布，那么$y = \mu + Lz$的均值为$\mu$，协方差为$\Sigma$。

显然，变换方法依赖于它能够进行计算所需的概率分布，并且能够求所需的概率分布的不定积分的反函数。这样的计算只对于一些非常有限的简单的概率分布可行，因此我们必须寻找一些更加一般的方法。这里，我们考虑两种方法，即拒绝采样（rejection sampling）和重要采样（importance sampling）。虽然这些方法主要限制在单变量概率分布，因此无法直接应用于多维的复杂问题，但是这些方法确实是更一般的方法的重要成分。