密度估计的核方法的一个问题是控制核宽度的参数对于所有核都是固定的。在高数据密度区域，大的值可能会导致过于平滑，且破坏了本应从数据中提取出的结构。但是，减小的值可能导致数据空间中低密度区域估计的噪声。所以的最优选择依赖于数据空间中的位置。这个问题可以由密度估计的近邻算法来解决。
因此，回到局部密度估计的一般结果（2.246），与之前固定然后从数据中确定的值不同，我们考虑固定的值然后使用数据来确定合适的值。为了达到这个目的，考虑一个以点为中心的小球体，我们希望估计密度，且允许球体的半径可以自由增加，直到它精确地包含个数据点。概率密度的估计就由式（2.246）给出，其中等于得到的球体的体积。这就是K近邻算法。图2.26展示了与图2.24、2.25相同的数据集下不同的K的选择。
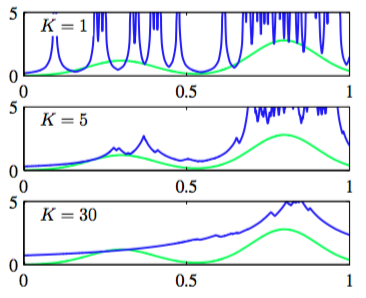
图 2.26 K近邻算法
我们看到现在的值控制了光滑的程度，且与之前一样，的最优选择既不能太大也不能太小。注意，由于对所有空间的积分是发散的，所以K近邻算法产生的模型不是真正的密度模型。
我们把密度估计的K近邻技术如何推广到分类问题作为本章的结束。为了达到这个目的，对每个独立的类别应用K近邻密度估计，然后在使用贝叶斯定理。假设有类别的数据点个，总共个点的数据集，即。如果想确定新数据点的分类，那么我们画一个以为中心的，正好包含个不论属于哪个类别的数据点的球体。这样，式（2.246）为每个类别提供了密度估计：
同样的，无条件概率密度为
其中类别的先验是由
给出。现在使用贝叶斯定理将式（2.253）、（2.254）和（2.255）结合起来，得到类别的后验概率：
如果希望误分类的概率最小，那么可以把测试点分配给有着最大后验概率的类别，对应着最大的。因此为了给新的数据点分类，我们从训练数据中选择个最近的数据点，然后把新的数据点分配为这个集合中数量最多的点的类别。特例，因为简单地把测试点分类为训练数据集里距离最近的数据点的类别，所以被称为最近邻规则(nearest-neighbour rule)，。图2.27展示了这些概念。
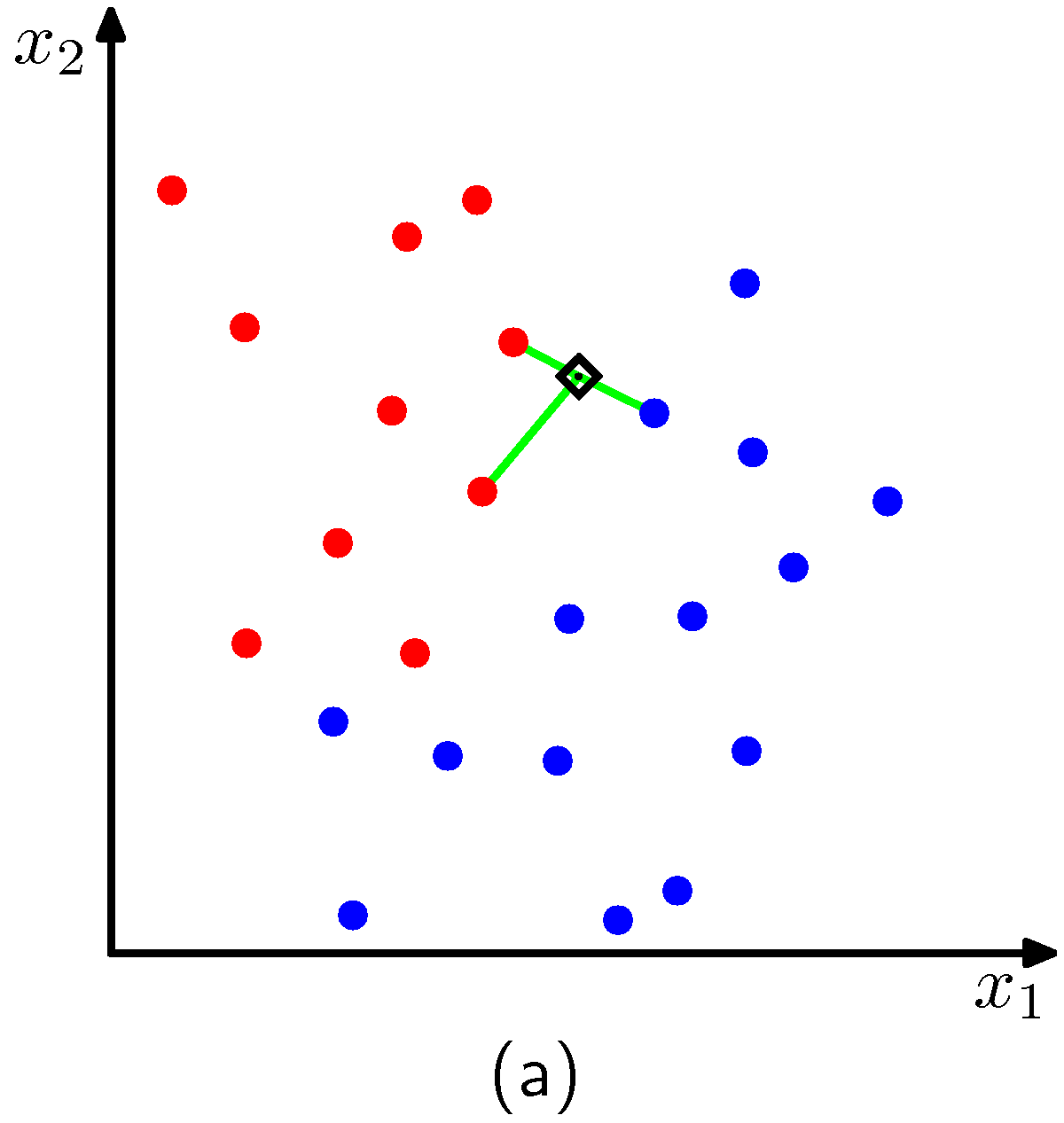
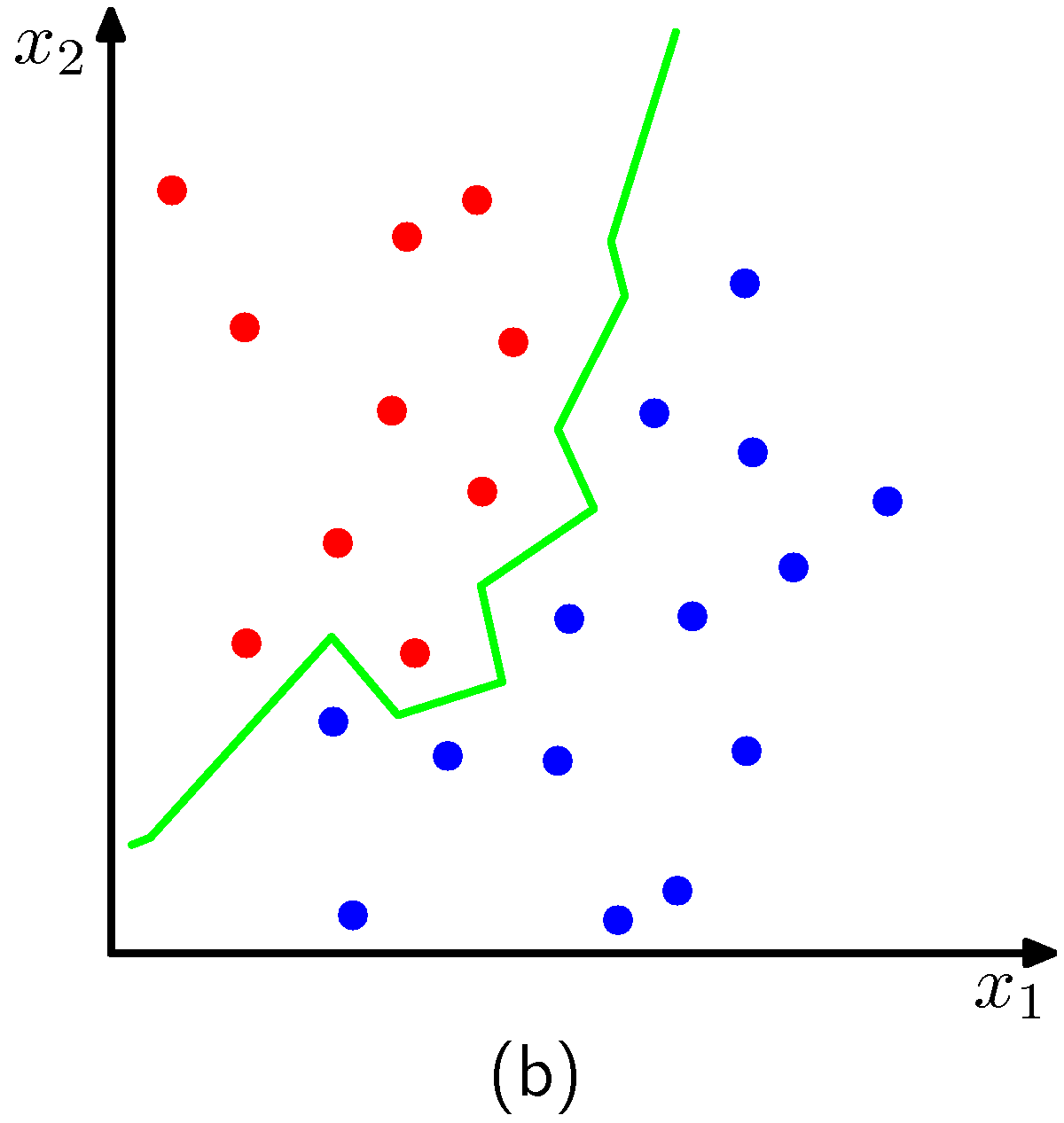图 2.27 K近邻分类
在图2.28中，展示了第一章中介绍的石油流数据集在不同的值下的近邻算法的结果。如我们期望的那样,控制着光滑度，即小的值会使得每个类别有许多小区域，而大的值会产生数量较少面积较大的区域。
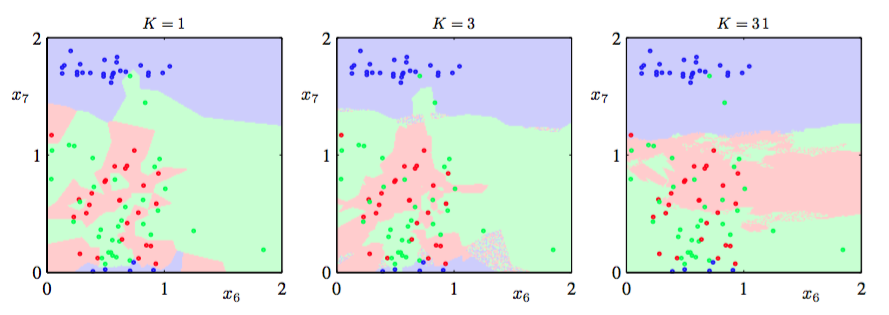
图 2.28 石油数据集的K近邻分类
最近邻(K = 1)分类器的一个有趣的性质是在极限的情况下，它的错误率不会超过最优分类器（即真实概率分布的分类器）可以达到的最小错误率的二倍（Cover and Hart, 1967）。
正如到目前为止讨论的那样，K近邻方法和核密度估计方法都需要存储整个训练数据，这导致计算大数据集会非常昂贵。通过一次额外的计算来构造一个基于树的搜素结构，使得可以不遍历整个数据集高效地找到（近似）近邻，这种计算代价可以被抵消。尽管这样，这些非参数化方法然有很大的局限性。另一方面，我们已经看到，简单的参数化模型非常受只能表示某一种形式的概率分布的限制。因此我们需要寻找一种非常灵活概率密度模型，且它的复杂度可以被控制为与训练数 据的规模无关。在后续章节中将会看到如何找到这种概率密度模型。