假设，我们的观测来自于$D$维欧式空间中的未知概率密度$p(x)$，希望估计出$p(x)$。根据之前对于局部性的讨论，让我们考虑包含$x$的小区域$R$。这个区域的概率质量是由

$$P = \int_Rp(x)dx \tag{2.242}$$

给出的。假设已经收集了服从分布$p(x)$的$N$次观测。由于每个数据点都有落在区域$R$中的概率$P$，所以位于区域$R$内部的数据点的总数$K$将服从二项分布

$$Bin(K|N,P) = \frac{N!}{K!(N-K)!}P^K(1-P)^{N-K} \tag{2.243}$$

使用式（2.11），得到落在区域内部的数据点的平均比例为$\mathbb{E}[K/N] = P$，同时引用式（2.12）得到这个均值的方差为$var[K/N] = P(1-P)/N$。对于大的$N$值，这个分布将会在均值附近产生尖峰，且

$$K \simeq NP \tag{2.244}$$

但是，如果同时假定区域$R$足够小，使得在这个区域内的概率密度$p(x)$大致为常数，那么就有

$$P \simeq p(x)V \tag{2.245}$$

其中$V$是$R$的体积。结合式（2.244）和（2.245）得到密度估计的形式：

$$p(x) = \frac{K}{NV} \tag{2.246}$$

注意，式（2.246）的成立依赖于两个相互矛盾的假设，即区域$R$要足够小，使得这个区域内的概率密度近似为常数，但是也要足够大（关于密度的值），使得落在这个区域内的数据点的数量$K$足够让二项分布达到尖峰。

有两种方法来利用式（2.246）的结果。可以固定$K$然后通过数据中确定$V$的值，这就是马上就要讨论的K临近算法。也可以固定$V$然后通过数据中确定$K$的值，这就是核方法。可以证明，在极限$N \to \infty$下，如果$V$ 随着$N$而合适地收缩，且$K$随着$N$增大，那么$K$近邻密度估计和核密度估计都会收敛到真实的概率密度(Duda and Hart, 1973)。

先详细讨论核方法。首先，我们把区域$R$取成以想确定概率密度的点$x$为中心的小超立方体。为了统计落在这个区域内的数据点的数量$K$，定义函数

$$k(u) = \begin{cases} 1, |u_i| \leq 1/2, i=1,...,D, \\ 0, otherwise \end{cases} \tag{2.247}$$

会比较方便。这表示一个以原点为中心的单位立方体。函数$k(u)$是核函数的一个例子。在这个问题中也被称为Parzen window。从式（2.247），如果数据点$x_n$位于以$x$为中心的边长为$h$的立方体中，那么量$k((x-x_n)/h)$等于1，否则它的值为0。位于这个立方体内的数据点的总数为：

$$K = \sum\limits_{n=1}^Nk\left(\frac{x-x_n}{h}\right) \tag{2.248}$$

把这个表达式代入式（2.246），可以得到点$x$处的概率密度估计

$$p(x) = \frac{1}{N}\sum\limits_{n=1}^N\frac{1}{h^D}k\left(\frac{x-x_n}{h}\right) \tag{2.249}$$

其中使用了$D$维边长为$h$的立方体的体积公式$V = h^D$。使用函数$k(u)$的对称性，可以重新解读这个等式为以$N$个数据点$x_n$为中心的$N$个立方体的和，而不是解读为以$x$为中心的一个立方体。

核密度估计（2.249）和之前的直方图方法一样会碰到人为带来的非连续性的问题。这个是由密度估计中立方体的边界带来的。如果我们选择一个平滑的核函数，那么就可以得到一个更加光滑的模型。一个常用的选择是高斯核函数，它给出

$$p(x) = \frac{1}{N}\sum\limits_{n=1}^N\frac{1}{(2\pi h^2)^{1/2}}exp\left\{-\frac{\Vert x-x_n\Vert^2}{2h^2}\right\} \tag{2.250}$$

核概率密度模型。其中$h$表示高斯分布的标准差。这个密度模型是通过使每个数据点服从高斯，然后把它们的贡献加起来得到的，之后除以$N$，使得概率密度被正确的标准化。图2.25中展示了把模型（2.250）应用于之前用来说明直方图方法的数据集上的图像。

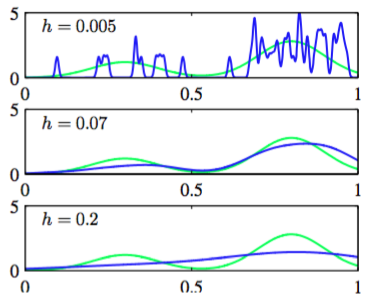
图 2.25 核密度模型的例子

看到，和我们期望的一样，参数$h$担当平滑参数的角色，且需要在，小的$h$会造成模型对噪声过于敏感,而大的$h$会造成过度平滑间做一个权衡。同样的，对$h$的优化是一个模型复杂度的问题，类似于直方图密度估计中对于箱子宽度的选择，也类似于曲线拟合问题中的多项式阶数。

要满足条件：

$$\begin{eqnarray} k(u) &\geq& 0, \tag{2.251} \\ \int k(u)du &=& 1 \tag{2.252} \end{eqnarray}$$

可以任意选择公式(2.249)中的核函数。这确保了最终求得的概率分布在处处都是非负的，且积分等于1。式（2.249）给出的这类密度模型被称为核密度估计，或Parzen估计。它的一个很大的优点是：因为“训练”阶段只需要存储训练集即可，所以它不需要进行“训练”阶段的计算。然而，这也是一个巨大的缺点，因为评估密度的计算代价随着数据集的规模线性增长。