在分类的概率方法中,我们的目标是在给定一组训练数据的情况下,对于一个新的输入向量,为目标变量的后验概率建模。这些概率一定位于区间中,而一个高斯过程模型做出的预测位于整个实数轴上。然而,我们可以很容易地通过使用一个恰当的非线性激活函数,将高斯过程的输出进行变换来调整高斯过程,使其能够处理分类问题。
首先考虑一个二分类问题,它的目标变量为。如果我们定义函数上的一个高斯过程,然后使用式(4.59)给出的logistic sigmoid函数进行变换,那么我们就得到了函数上的一个非高斯随机过程,其中。图6.11说明了一维输入空间的情况,其中目标变量上的概率分布是伯努利分布
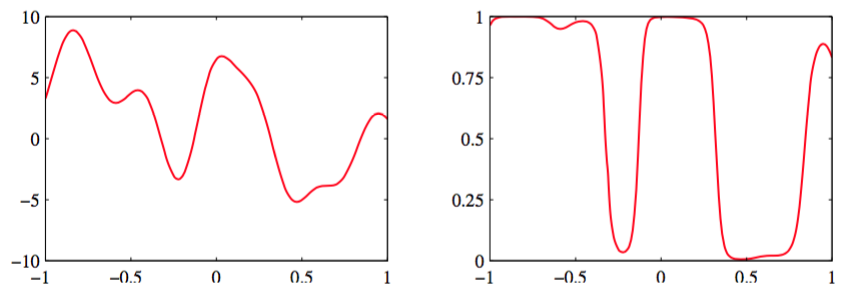
图 6.11 左图给出了在函数上定义了一个高斯过程先验的样本,右图给出了使用logistic sigmoid对这 个样本进行变换得到的结果。
与之前一样,我们把训练集的输入记作,对应的观测目标变量为。我们还考虑一个单一的测试数据点,目标值为。我们的目标是确定预测分布,其中我们没有显式地写出它对于输入变量的条件依赖。为了完成这个目标,我们引入向量上的高斯过程先验,它的分量为。这反过来定义了上的一个非高斯过程。通过以训练数据为条件,我们得到了求解的预测分布。上的高斯过程先验的形式为
与回归的情形不同,协方差矩阵不再包含噪声项,因为我们假设所有的训练数据点都被正确标记。然而,由于数值计算的原因,更方便的做法是引入一个由参数控制的类似噪声的项,它确保了协方差矩阵是正定的。因此协方差矩阵的元素为
其中是6.2节讨论的一个任意的半正定核函数,的值通常事先固定。我们会假定核函数由参数向量控制,我们稍后会讨论如何从训练数据中学习到。
对于二分类问题,预测就足够了,因为的值等于。求解的预测分布为
其中。
这个积分无法求出解析解,因此可以使用采样的方法近似(Neal, 1997)。我们还可以使用另一种基于一个解析的近似的方法。在4.5.2节,我们推导了logistic sigmoid函数与高斯 分布卷积的近似公式(4.153)。我们可以使用这个结果计算公式(6.76)中的积分,只要我们对后验概率分布进行高斯近似。通常对后验概率进行高斯近似的理由是,根据中心极限定理,随着数据点数量的增加,真实的后验概率将会趋向于一个高斯分布。在高斯过程的情形中,变量的数量随着数据点数量的增多而增多,因此这个结果不能直接应用。然而,如果我们考虑增加落在x空间的固定区域中的数据点的数量,那么函数中对应的不确定性就会减小,这就渐近地趋近于高斯分布(Williams and Barber, 1998)。
我们考虑三种不同的获得高斯近似的方法。一种方法基于变分推断(variational inference)(Gibbs and MacKay, 2000),并且使用了logistic sigmoid函数的局部变分界(10.144)。这使得sigmoid函数的乘积可以通过高斯的乘积近似,因此使得对的积分可以解析地计算。这种方法也产生了似然函数的下界。通过使用softmax函数的高斯近似,高斯过程分类的变分法框架也可以扩展到多类问题)Gibbs, 1997)。
第二种方法使用期望传播(expectation propagation)(Opper and Winther, 2000b; Minka, 2001b; Seeger, 2003)。正如我们将看到的那样,由于真实的后验概率是单峰的,期望传播方法可以给出很好的结果。