我们可以使用二值图像中图像去噪的例子来说明无向图的应用(Besag, 1974; Geman and Geman, 1984; Besag, 1986)。虽然这是一个非常简单的例子,但是它可以代表许多更复杂的应用。我们令观测的噪声图像通过一个二值像素值组成的数组来描述,其中下标覆盖了所有的像素。我们假设图像通过取一张未知的无噪声图像,这幅图像由二值像素值描述,然后以一个较小的概率随机翻转像素值的符号的方式获得。图8.30给出了一个二值图像以及一副噪声图像,其中噪声图像中像素值发生符号翻转的概率为10%。

图 8.30 使用马尔科夫随机场进行图像去噪的例子。上面一行中,左侧是原始的二值图像,右侧是随机改变10%的像素后得到的带有噪声的图像。下面一行中,左图是使用迭代条件模型(ICM)恢复的图像,右图是使用最大割算法得到的图像。ICM产生的图像中,96%的像素与原始图像相符,而最大割算法产生的图像中,这个比例为99%。
给定带有噪声的图像,我们的目标是恢复原始的无噪声的图像。
由于噪声等级比较小,因此我们知道xi和yi之间有着强烈的相关性。我们还知道图像中相邻像素的相关性很强。这种先验知识可以使用马尔科夫随机场模型进行描述,它的无向图如图8.31所示。
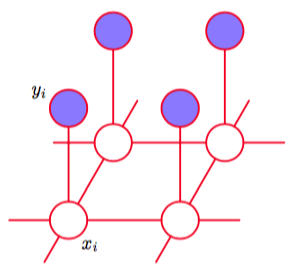
图 8.31 一个无向图模型,表示图像去噪的马尔科夫随机场,其中是一个二值变量,表示像素在一个未知的无噪声的图像中的状态,表示在观测到的噪声图像中,像素的对应值。
这个图中有两种类型的团块,每一种团块包含两个变量。形如的团块有一个关联的能量函数,表达了这些变量之间的相关性。对于这些团块,我们选择一个非常简单的能量函数,其中是一个正的常数。这个能量函数具有当符号相同时,能量函数会给出一个较低的能量(即较高的概率),而当符号相反时,能量函数会给出一个较高的能量的效果。
剩余的团块由变量组成,其中是相邻像素的下标。与之前一样,我们希望当两个像素符号相同时能量较低,当两个像素符号相反时能量较高,因此我们选择能量函数,其中是一个正的常数。
由于势函数是最大团块上的一个任意的非负的函数,因此我们可以将势函数与团块的子集上的任意非负函数相乘,或等价的,我们可以加上对应的能量。在这个例子中,这使得我们可以为无噪声图像的每个像素加上一个额外的项。这样的项具有将模型进行偏置,使得模型倾向于选择一个特定的符号,而不选择另一个符号的效果。
于是,模型的完整的能量函数的形式为
它定义了上的一个联合概率分布,形式为
我们现在固定噪声图像的像素给出的观测值y的元素,这个噪声图像隐式地定义了一个无噪声图像上的条件概率分布。这是Ising模型的一个例子,这个模型在统计物理学中被广泛研究。为了恢复图像,我们希望找到一个具有较高概率(理想情况下具有最高概率)的图像。 为了完成这件事,我们要使用一个简单的迭代方法,叫做迭代条件峰值(iterated conditional model),或称为ICM(Kittler and Foglein, 1984)。这种方法仅仅是坐标间的梯度上升方法的一个应用。这种方法的思想是,首先初始化变量,这个过程中我们只是简单地令对于所有都成立。然后,我们每次取一个结点,计算两个可能状态和的总能量,保持其他所有结点变量固定,将设置为能量较低的状态。如果不变,则概率不变,否则概率就会增大。由于只有一个变量发生改变,因此这是一个可以高效进行的简单局部计算。然后,我们对其他的结点重复更新过程,以此类推,知道满足某个合适的停止条件。结点可以用一种系统的方式更新,例如重复地依次扫描图像,或随机地选择结点。
如果我们有一个更新的顺序,使得每个像素都至少被访问一次,且没有变量发生改变,那么根据定义,算法会收敛于概率的一个局部最大值。然而,这未必对应于全局最大值。
对于这个简单的例子来说,我们将参数固定为。注意,令意味着两个状态的先验概率是相等的。首先,我们使用噪声图像进行初始化,然后运行ICM直到收敛,得到了图8.30左下角的去噪图像。注意,如果我们令,从而去除了相邻像素点之间的联系,那么整体概率最大的解为(对于所有的),这对应于观测到的噪声图像。
稍后,我们会讨论一种更加高效的算法寻找高概率的解,这种算法被称为最大加和算法,它通常会产生更好的解,虽然这种算法仍然不保证找到后验概率的全局最大值。然而,对于某类模型,包括由式(8.42)给出的模型,存在基于图割(graph cut)的高效的算法,保证找到全局的最大值(Greig et al., 1989; Boykov et al., 2001; Kolmogorov and Zabih, 2004)。图8.30的右下角给出了将图割算法应用于去噪问题的结果。