目前为止，我们已经介绍了信息论的许多概念，包括熵的关键思想。我们现在开始把这些思想关联到模式识别的问题中。考虑某个未知的分布$p(x)$，假定我们已经使用一个近似的分布$q(x)$对它进行了建模。如果我们使用$q(x)$来建立一个编码体系，用来把$x$的值传给接收者，那么，由于我们使用了$q(x)$而不是真实分布$p(x)$，因此在具体化$x$的值(假定我们选择了一个高效的编码系统)时，需要一些附加的信息。需要的平均的附加信息量(单位是nat)为：

$$\begin{eqnarray} KL(p||q) &=& -\int p(x) \ln q(x)dx - \left(-\int p(x)\ln p(x)dx\right) \\ &=& -\int p(x)\ln\left\{\frac{q(x)}{p(x)}\right\}dx \tag{1.113} \end{eqnarray}$$

这被称为分布$p(x)$和分布$q(x)$之间的相对熵(relative entropy) 或者Kullback-Leibler散度 (Kullback-Leibler divergence)，或者KL散度(Kullback and Leibler, 1951)。注意这不是一个对称量，即$KL(p||q) \not\equiv KL(q||p)$。

现在要证明，Kullback-Leibler散度满足$KL(p || q) \geq 0$，并且当且仅当$p(x) = q(x)$时等号成立。为了证明这一点，我们首先介绍凸函数(convex function)的概念。如果一个函数具有如下性质：每条弦都位于函数图像或其上方(如图1.31所示)，那么我们说这个函数是凸函数。

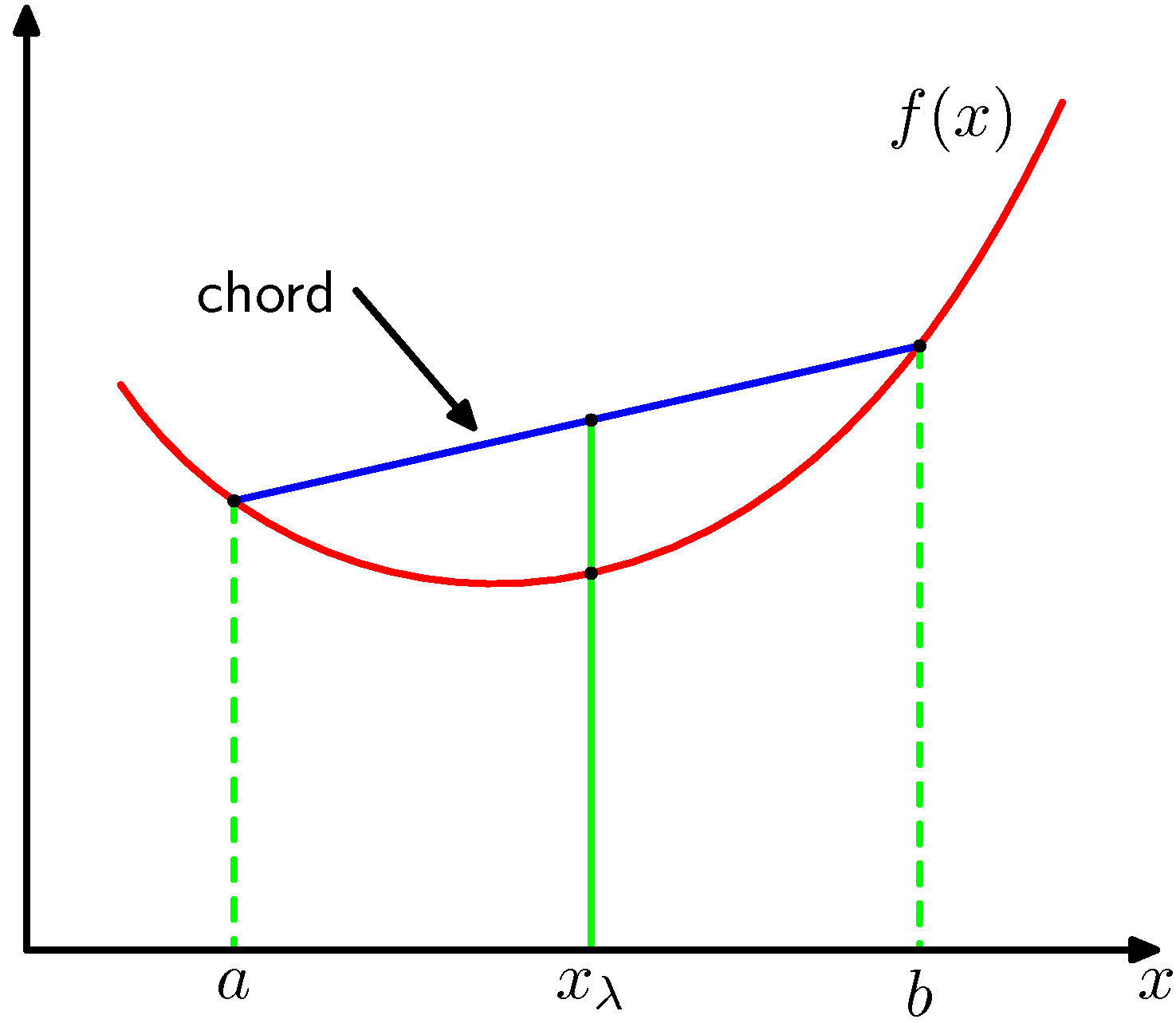
图 1.31 凸函数$f(x)$的每条弦（蓝色表示）位于函数上或函数上方，函数用红色曲线表示。

位于$x = a$到$x = b$之间的任何一个$x$值都可以写成$\lambda a + (1 − \lambda)b$的形式，其中$0 ≤ \lambda ≤ 1$。弦上的对应点可以写成$\lambda f (a) + (1 − \lambda )f (b)$，函数的对应值为$f (\lambda a + (1 − \lambda )b)$。这样，凸函数的性质就可以表示为

$$f(\lambda a + (1 − \lambda )b) ≤ \lambda f(a) + (1 − \lambda)f(b) \tag{1.114}$$

这等价于要求函数的二阶导数处处为正。凸函数的例子有$x\ln x(x > 0)$和$x^2$。如果等号只在$\lambda = 0$和$\lambda = 1$处取得，我们就说这个函数是严格凸函数(strictly convex function)。如果一个函数具有相反的性质，即每条弦都位于函数图像或其下方，那么这个函数被称为凹函数 (concave function)。对应地，也有严格凹函数(strictly concave function)的定义。如果$f(x)$是凸函数，那么$−f (x)$就是凹函数。

使用归纳法，我们可以根据公式(1.114)证明凸函数$f(x)$满足

$$f(\sum\limits_{i=1}{M}\lambda_ix_i) \leq \sum\limits_{i=1}{M}\lambda_if(x_i) \tag{1.115}$$

其中，对于任意点集$\{x_i\}$。都有$\lambda_i \geq 0$且 $\sum_i\lambda_i = 1$。公式(1.115)的结果被称为Jensen不等式（Jensen's inequality）。如果我们把$\lambda_i$看成取值为$\{x_i\}$的离散变量x的概率分布，那么公式(1.115)就可以写成

$$f(\mathbb{E}[x]) \leq \mathbb{E}[f(x)] \tag{1.116}$$

其中，$\mathbb{E}[·]$表示期望。对于连续变量，Jensen不等式的形式为

$$f\left(\int xp(x)dx\right) \leq \int f(x)p(x)dx \tag{1.117}$$

我们把公式(1.117)形式的Jensen不等式应用于公式(1.113)给出的Kullback-Leibler散度，可得

$$KL(p||q) = -\int p(x)\ln \left\{\frac{q(x)}{p(x)}\right\}dx \geq -\ln \int q(x)dx = 0 \tag{1.118}$$

推导过程中，我们使用了$−\ln x$是凸函数的事实，以及标准化条件$q(x)dx = 1$。实际上，$−\ln x$是严格凸函数，因此只有$q(x) = p(x)$对于所有x都成立时，等号才成立。因此我们可以把Kullback-Leibler散度看做两个分布$p(x)$和$q(x)$之间不相似程度的度量。

我们看到，在数据压缩和密度估计（即对未知概率分布建模）之间有一种隐含的关系，因为当我们知道真实的概率分布之后，我们可以给出最有效的压缩。如果我们使用了不同于真实分布的概率分布，那么我们一定会损失编码效率，并且在传输时增加的平均额外信息量至少等于两个分布之间的Kullback-Leibler散度。

假设数据通过未知分布$p(x)$生成，我们想要对$p(x)$建模。我们可以试着使用一些参数分布$q(x | θ)$来近似这个分布。$q(x | \theta)$由可调节的参数$\theta$控制(例如一个多元高斯分布)。一种确定$\theta$的方式是最小化$p(x)$和$q(x | \theta)$之间关于$\theta$的Kullback-Leibler散度。我们不能直接这么做，因为我们不知道$p(x)$。但是，假设我们已经观察到了服从分布p(x)的有限数量的训练点$x_n$，其中$n = 1,...,N$。那么，关于$p(x)$的期望就可以通过这些点的有限加和，使用公式(1.35)来近似，即

$$KL(p||q) \simeq \sum\limits_{n=1}^{N}\{-\ln q(x_n|\theta) + \ln p(x_n)\} \tag{1.119}$$

右侧的第二项与$\theta$无关，第一项是使用训练集估计的分布$q(x|\theta)$下的$\theta$的负对数似然函数。因此我们看到，最小化Kullback-Leibler散度等价于最大化似然函数。

现在考虑由$p(x, y)$给出的两个变量x和y组成的数据集。如果变量的集合是独立的，那么他们的联合分布可以分解为边缘分布的乘积$p(x, y) = p(x)p(y)$。如果变量不是独立的，那么我们可以通过考察联合概率分布与边缘概率分布乘积之间的Kullback-Leibler散度来判断它们是否“接近”于相互独立。此时，Kullback-Leibler散度为

$$\begin{eqnarray} I[x,y] &\equiv& KL(p(x, y) \Vert p(x)p(y)) \\ &=& −\int\int p(x,y)\ln(\frac{p(x)p(y)}{p(x,y)})dxdy \tag{1.120} \end{eqnarray}$$

这被称为变量$x, y$之间的互信息(mutual information)。根据Kullback-Leibler散度的性质，我们看到$I[x, y] \geq 0$，当且仅当$x, y$相互独立时等号成立。使用概率的加法和乘法规则，我们看到互信息和条件熵之间的关系为

$$I[x, y] = H[x] − H[x|y] = H[y] − H[y|x]$$

因此我们可以把互信息看成由于知道y值而造成的x的不确定性的减小（反之亦然）。从贝叶斯的观点来看，我们可以把$p(x)$看成$x$的先验概率分布，把$p(x|y)$看成我们观察到新数据$y$之后的后验概率分布。因此互信息表示一个新的观测$y$引起的x的不确定性的减小。