我们对高斯分布参数的最大似然估计的讨论，给我们更方便的讨论更一般的最大似然顺序估计主题提供机会。顺序方法允许我们一次处理一个数据然后丢弃掉，这对于线上应用来说很重要，而且对于大数据集来说一次批量处理所有的数据是不太可能的。

考虑式（2.121）的均值的最大似然估计$\mu_{ML}$，把基于$N$个观察量的估计记作$\mu_{ML}^{(N)}$ 。分析最后一个数据点$x_N$的贡献得到：

$$\begin{eqnarray} \mu_{ML}^{(N)} &=& \frac{1}{N}\sum\limits_{n=1}^Nx_n \\ &=& \frac{1}{N}x_N + \frac{1}{N}\sum\limits_{n=1}^{N-1}x_n \\ &=& \frac{1}{N}x_N + \frac{N-1}{N}\mu_{ML}^{(N-1)} \\ &=& \mu_{ML}^{(N-1)} + \frac{1}{N}(x_N - \mu_{ML}^{(N-1)}) \tag{2.126} \end{eqnarray}$$

接下来讨论这结果的非常棒的解释。观察到$N - 1$个点之后，我们用$\mu_{ML}^{(N - 1)}$来估计$\mu$。现在我们观测到点$x_N$，然后，我们沿着“错误信号”$(x_N - \mu_{ML}^{(N - 1)})$方向移动估计$1/N$的微小的量来修正后的估计$\mu_{ML}^{(N)}$ 。注意$N$在变大，所以连续数据点的贡献也变得越来越小。

式（2.126）的结果显然与式（2.121）的批量结果一样，因为这两个公式相等。但是，我们不是总能使用这种方法推导出一个顺序的算法，这就需要找到一种更通用的顺序学习方法，这就是Robbins-Monro算法。考虑一对有联合分布$p(z, \theta)$控制的随机变量$\theta , z$。$\theta$上的$z$的条件期望由确定函数$f(\theta)$给出：

$f(\theta) \equiv \mathbb{E}[z|\theta] = \int zp(z|\theta) dz \tag{2.127}$

图2.10给出了图形化的说明。通过这种方式定义的函数被称为回归函数(regression function)。

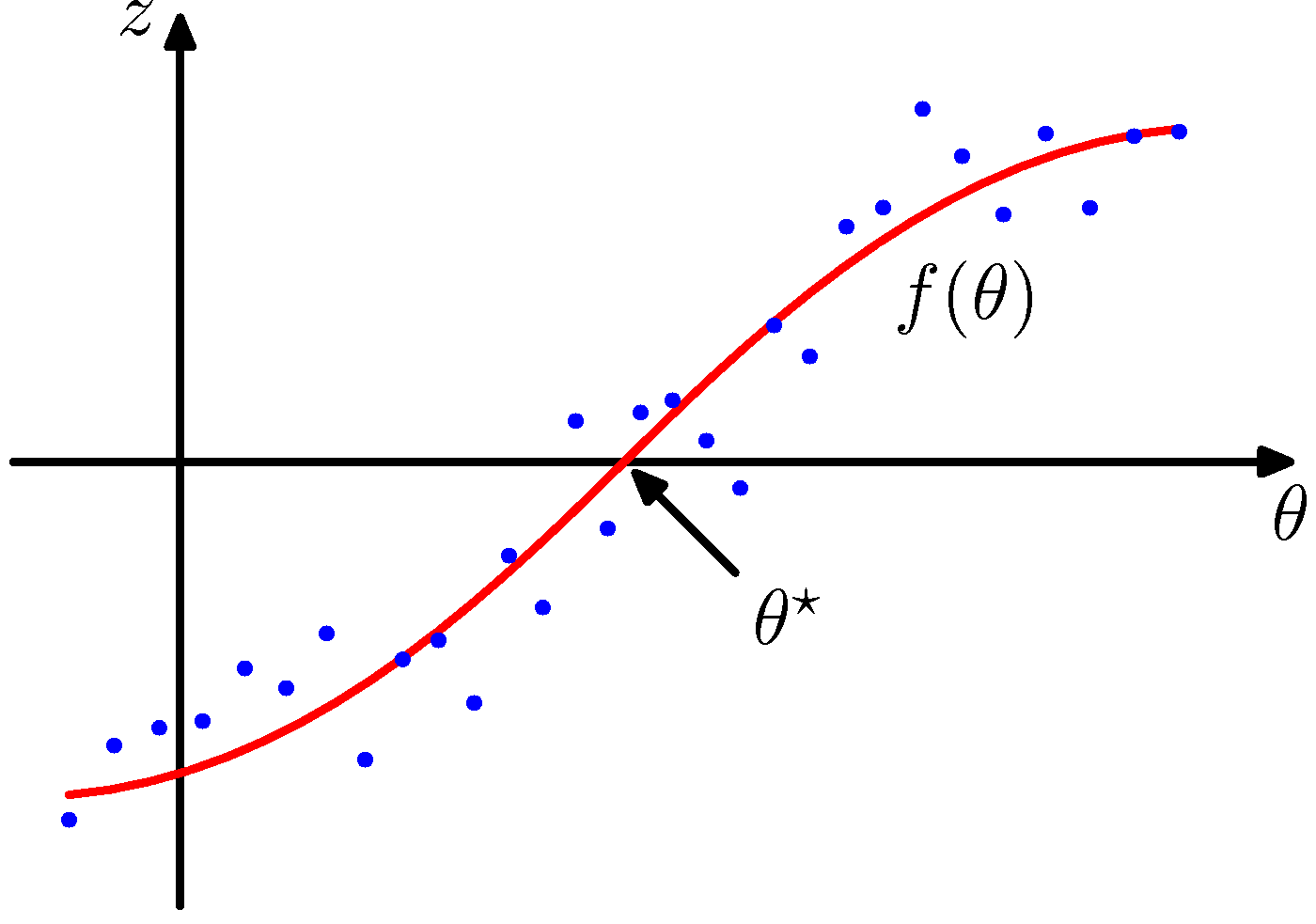
图 2.10 两个相关的随机变量$z$和$\theta$以及由条件期望$E[z|\theta]$给出的回归函数$f(\theta)$的图形表示。Robbins-Monro算法提供了一个一般的顺序步骤来寻找这种函数的根$\theta^*$。

我们的目标是求使得$f(\theta^*) = 0$的根$\theta^*$。如果我们有大量的$z, \theta$的观测数据集，那么我们可以直接对回归函数建模，得到根的一个估计。但是，假设一次只能一个$z$的观测值，那个就需要一个对应的顺序估计方法来找到$\theta^*$。下面这种解决这样的问题的通用方法是由Robbins and Monro (1951)给出的。假定$z$的条件方差是有限的：

$\mathbb{E}[(z-f)^2|\theta] < \infty \tag{2.128}$

并且不失一般性的假设当$\theta > \theta^∗$时$f(\theta) > 0$,当$\theta < \theta^∗$时$f(\theta) < 0$，如图2.10所示。Robbins-Monro方法定义了对根$\theta^*$的一系列顺序估计：

$\theta^{(N)} = \theta^{(N-1)} + a_{N-1}z(\theta^{(N-1)}) \tag{2.129}$

其中$z(\theta^{(N)})$是当$\theta$取$\theta^{(N)}$时$z$的观测值。系数$\{a_N\}$表示一个满足下列条件的正数序列：

$$\begin{eqnarray} \lim\limits_{N \to \infty}a_N &=& 0 \tag{2.130} \\ \sum\limits_{N=1}^\infty a_N &=& \infty \tag{2.131} \\ \sum\limits_{N=1}^\infty a_N^2 &<& \infty \tag{2.132} \end{eqnarray}$$

可以证明式（2.129）给出的一系列估计以概率1收敛到根（Robbins and Monro, 1951; Fukunaga, 1990）。注意，第一个条件（2.130）保证连续修正的幅度变小使得它能收敛到极限值。第二个条件（2.131）保证算法不会收敛不到根的值。第三个条件（2.132）保证了累计噪声有一个有限的方差，使它不破坏收敛性。

现在，我们讨论Robbins-Monro算法如何解决一般的顺序最大似然问题。根据定义，最大似然解$\theta_{ML}$是对数似然函数的驻点。因此满足：

$$\frac{\partial}{\partial\theta}\left\{\frac{1}{N}\sum\limits_{n=1}^N\ln p(x_n|\theta) \right\}\Bigg\vert_{\theta_{ML}} = 0 \tag{2.133}$$

交换求导与求和顺序，且令极限$N \to \infty$得到：

$$\lim\limits_{N \to \infty}\frac{1}{N}\sum\limits_{n=1}^N\frac{\partial}{\partial\theta}\ln p(x_n|\theta) = \mathbb{E}_x\left[\frac{\partial}{\partial\theta}\ln p(x_n|\theta)\right] \tag{2.134}$$

所以求最大似然的解对应求解回归函数的根。因此我们可以应用Robbins-Monro方法，现在，它的公式是：

$$\theta^{(N)} = \theta^{(N-1)} + a_{N-1}\frac{\partial}{\partial\theta^{(N-1)}}\ln p(x_N|\theta^{(N-1)}) \tag{2.135}$$

作为一个特殊的例子，再次考虑高斯分布均值的顺序估计问题。在这种情况下,参数$\theta^{(N)}$是高斯分布均值$\mu_{ML}^{(N)}$的估计，随机变量$z$的形式为：

$$z = \frac{\partial}{\partial\mu_{ML}}\ln p(x|\mu_{ML}, \sigma^2) = \frac{1}{\sigma^2}(x-\mu_{ML}) \tag{2.136}$$

因此$z$是均值为$\mu - \mu_{ML}$的高斯分布，如图2.11展示。

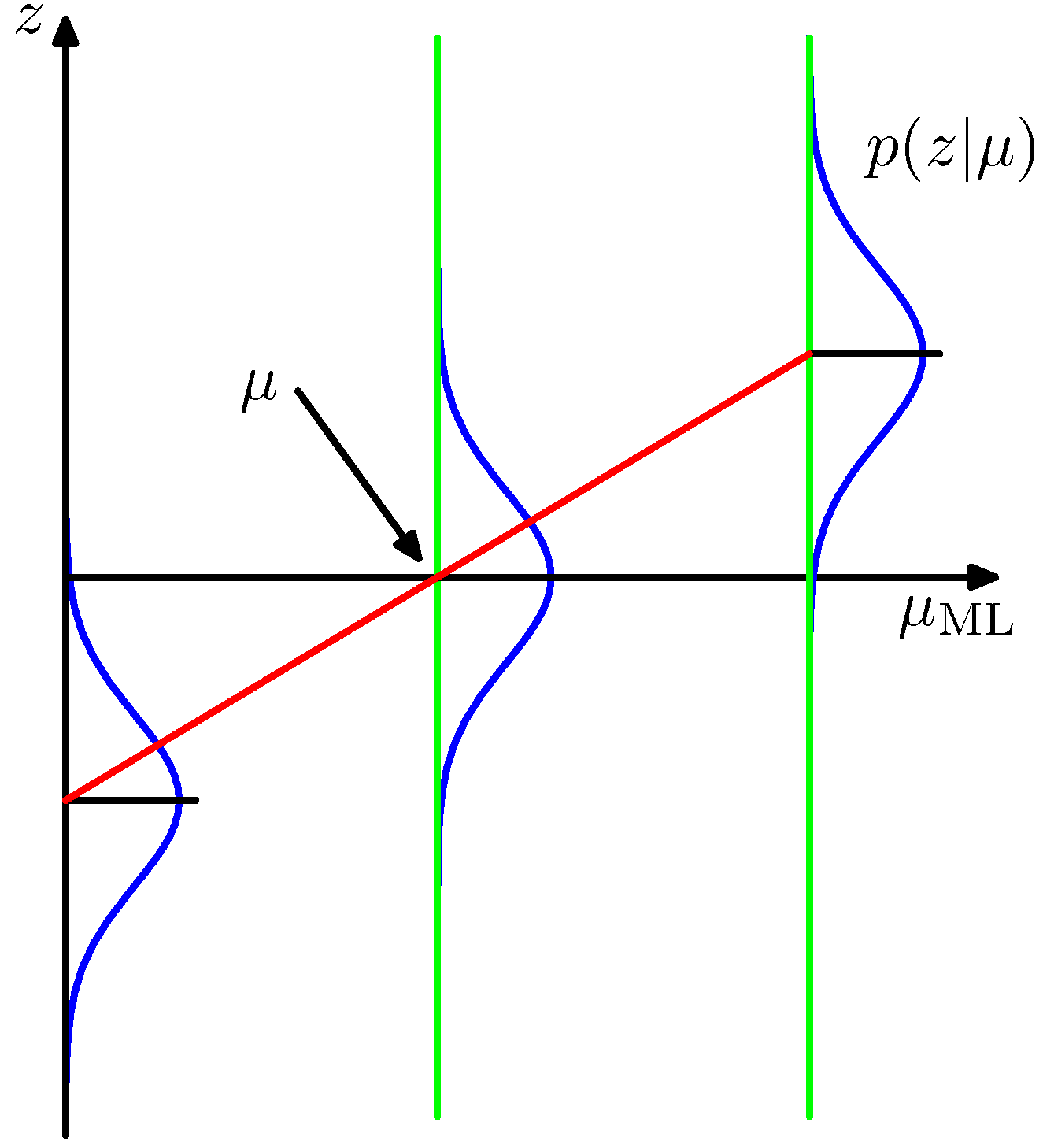
图 2.11 在高斯分布的情形中，图2.10所示的回归函数的形式是一条直线，用红色标记出，其中$\theta$对应于$\mu_{ML}$。在这种情况下，随机变量$z$对应于对数似然函数的导数，由$−(x − \mu_{ML})/\sigma^2$给出，定义了回归函数的期望是一条直线，由$−(\mu − \mu_{ML})/\sigma^2$给出。回归函数的根对应于真实的均值$\mu$。

把式（2.136）代入式（2.135）得到具有参数$a_N = \sigma^2 / N$的一元变量形式的（2.126）。虽然我们只讨论了一元变量的情形，同样的技术，以及式（2.130）-（2.132）给出的关于系数$a_N$的限制，同样适用于多元变量的情形(Blum, 1965)。