我们现在考虑图模型中的推断问题,图中的一些结点被限制为观测值,我们想要计算其他结点中的一个或多个子集的后验概率分布。正如我们将看到的那样,我们可以利用图结构找到高 效的推断算法,也可以让这些算法的结构变得透明。具体来说,我们会看到许多算法可以用图中局部信息传播的方式表示。本节中,我们会把注意力主要集中于精确推断的方法。在第10章中,我们会考虑许多近似推断的算法。
首先,让我们考虑贝叶斯定理的图表示。假设我们将两个变量x和y上的联合概率分布分解为因子的乘积的形式。这可以用图8.37(a)中的有向图表示。 现在假设我们观测到了的值,如图8.37(b)中的阴影结点所示。
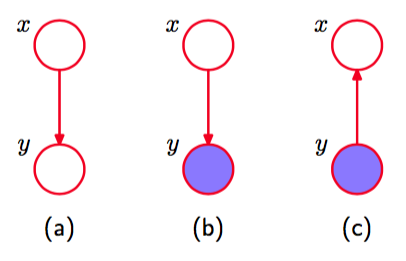
图 8.37 贝叶斯定理的图表示。
我们可以将边缘概率分布看成潜在变量上的先验概率分布,我们的目标是推断上对应的后验概率分布。使用概率的加和规则和乘积规则,我们可以计算
然后,这个式子被用于贝叶斯定理中,计算
因此现在联合概率分布可以通过和。从图的角度看,联合概率分布现在可以表示为图8.37(c)所示的图,其中箭头的方向翻转了。这是图模型中推断问题的最简单的例子。