考虑局部二次近似可以让我们更深入的认识最优化问题，得到更多解决这个问题的技术。

考虑$E(w)$在权空间中某个点$\hat{w}$处的泰勒展开

$$E(w) \simeq E(\hat{w}) + (w-\hat{w})^Tb + \frac{1}{2}(w-\hat{w})^TH(w-\hat{w}) \tag{5.28}$$

其中我们省略了立方和更高阶的项。这里定义$b$为$E$的梯度在$\hat{w}$处的值

$$b \equiv \nabla E|_{w=\hat{w}} \tag{5.29}$$

且Hessian矩阵$H = \nabla\nabla E$具元素

$$(H)_{ij} \equiv \left.\frac{\parital E}{\partial w_i\partial w_j}\vphantom{\Big|}\right|_{w=\hat{w}} \tag{5.30}$$

根据式（5.28）梯度对应的局部近似由

$$\nabla E \simeq b + H(w-\hat{w}) \tag{5.31}$$

对于距离$\hat{w}$充分近的点$w$，这些表达式对误差函数和它的梯度给出了合理的近似。

考虑在误差函数最小值的点$w^*$附近的局部二次近似的特殊情况。这种情况下，由于在$w^*$处$\nabla E = 0$，所以没有线性项，式（5.28）变成

$$E(w) = E(w^*) + \frac{1}{2}(w-w^*)^TH(w-w^*) \tag{5.32}$$

其中Hessian矩阵$H$是在$w^*$处计算的。为了以几何方式来解释，考虑Hessian矩阵的特征方程

$$Hu_i = \lambda_iu_i \tag{5.33}$$

其中特征向量$u_i$构成了完备正交集（附录C），即

$$u_i^Tu_j = \delta_{ij} \tag{5.34}$$

现在，我们展开$(w - w^*)$得到特征向量的线性组合形式

$$w - w^* = \sum\limits_i \alpha_iu_i \tag{5.35}$$

这可以解释成，原点变成了点$w^*$，并旋转坐标轴与特征向量对齐（通过以$u_i$为列的正交矩阵）的坐标系统变换，在附录C中有更详细的讨论。把式（5.35）代入式（5.32）并使用式（5.33）及（5.34）得到误差函数可以写成

$$E(w) = E(w^*) + \frac{1}{2}\sum\limits_i\lambda_i\alpha_i^2 \tag{5.36}$$

的形式。

矩阵$H$是正定的，当且仅当

$$v^THv > 0, for all v \neq 0 \tag{5.37}$$

因为特征向量$\{u_i\}$组成了一个完备集，所以任意一个向量$v$都可以写成

$$v = \sum\limits_ic_iu_i \tag{5.38}$$

的形式。

根据（5.33）（5.34）得到

$$v^THv = \sum\limits_ic_i^2\lambda_i \tag{5.39}$$

所以，当且仅当所有特征值为正的时候$H$是正定的。图5.6展示了，在新的坐标系统中，基向量由特征向量$\{u_i\}$给出，$E$的等高线是以原点为中心的椭圆。

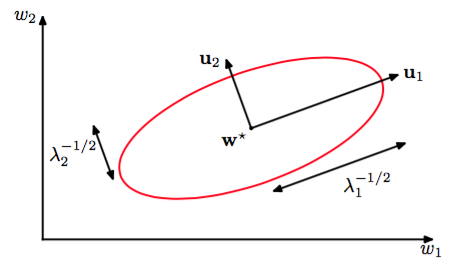
图 5.6 在最小值$w^*$的邻域中，误差函数的二次函数近似

对于1维权空间，当

$$\left.\frac{\partial^2E}{\partial w^2}\vphantom{\Big|}\right| _{w^*} > 0 \tag{5.40}$$

时，驻点$w^*$是最小值。对于$D$维权空间$w^*$处的Hessian矩阵是正定时，驻点$w^*$是最小值。