我们已经知道怎么把多项式拟合问题表示为误差最小化问题。现在我们回到曲线拟合的例子,并以概率的角度来看待,以及让我们完全从贝叶斯的角度来看待这个问题,从而更深刻地认识误差函数和正则化。
曲线拟合问题的目标是能够根据个输入组成的数据集和它们对应的目标值,在给出新的输入变量的新值的情况下,预测目标变量。我们可以用目标变量值的概率分布来表示我们的不确定性。为了这个目标,我们可以假设,对于给定的的值,对应的目标变量是具有与公式(1.1)给出的多项式曲线的值相等的均值的高斯分布,即:
其中,为了和后续章节记号的一致性,我们定义的分布的方差的逆为精度(precision)参数。图1.16阐述了这种模式。
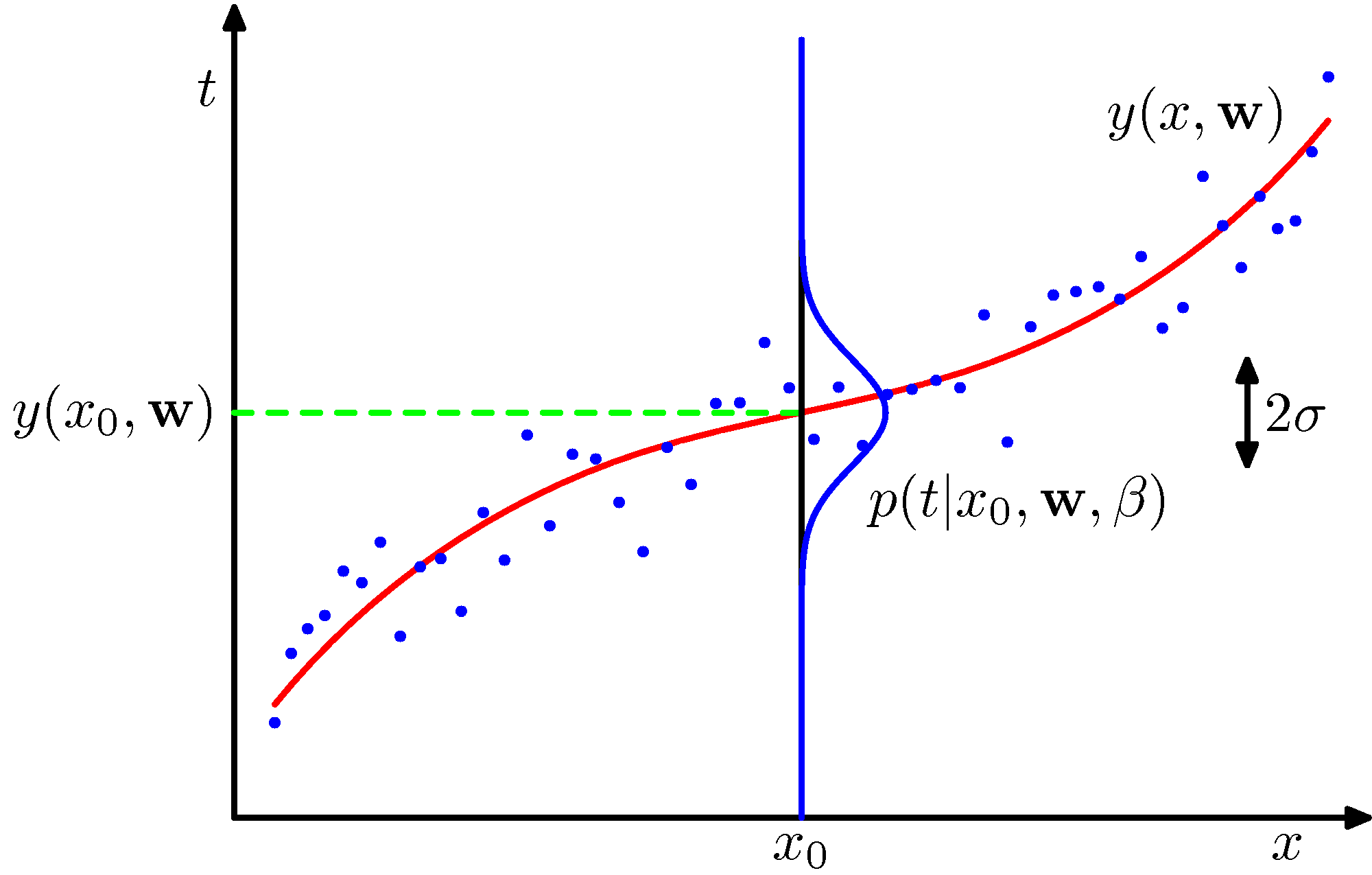
图 1.16: 目标值的高斯分布
现在,使用训练数据,并通过最大似然来确定未知参数。假定数据从(1.60)分布中独立的取出,那么似然函数就等于:
与之前处理简单高斯分布时的做法一样,为了方便,把它转化为最大化似然函数的对数。代入(1.46)给出的高斯分布公式,可以得到似然函数的对数形式:
首先考虑确定多项式系数的最大似然解,记作。它们是由对(1.62)关于的最大化来确定的。为了达到这个目的,可以先省略式(1.62)右手边的最后两项,因为它们与无关。并且,使用一个正系数来缩放似然函数的对数并不会改变它关于的最大值的位置,所以我们可以使用 1/2来代替。最后,等价地去最小化似然函数的负对数,来替代最大化似然函数的对数。于是得到,对于确定的最大化似然等价于(1.2)中给出的最小化平方和误差函数。所以,平方和误差函数是采用高斯噪声的最大似然的自然结果。
同样,可以使用最大似然来确定高斯条件分布的精度参数。关于来最大化公式(1.62)得到:
再次提醒,和简单的高斯分布情况一样,首先确定控制均值的参数向量,然后使用这个结果来确定精度。
当确定好参数后,就可以对新的值做预测。由于现在有了概率模型,所以可以使用一种称为预测分布(predictive distribution)来表达的概率分布,来代替一个简单的点估计。这是通过把最大似然参数代入式(1.60)得到的:
现在让我们朝着贝叶斯的方法前进一步,在多项式系数上引入先验分布。简单起见,我们考虑高斯分布:
其中是分布的精度,是阶多项式的向量中元素个数。像这样的控制分布的模型参数被称为超参数(hyperparameters)。使用贝叶斯定理,的后验分布,正比于先验分布和似然函数的乘积:
对于给定的数据集,可以通过找到最可能的值来确定,即最大化后验分布。这种技术叫做最大后验(maximum posterior)或简写为MAP。取公式(1.66)的负对数,结合公式(1.62)和 公式(1.65),我们可以看到,最大化后验概率就是最小化下式:
因此,最大化后验概率等价于最小化正则化的平方和误差函数(之前在公式(1.4)中提到),正则化参数为。