我们现在使用一元变量上的高斯分布来说明分解变分近似(MacKay, 2003)。我们的目标是在给定的观测值的数据集的情况下,推断均值和精度的后验概率分布。其中,我们假设数据是独立地从高斯分布中抽取的。似然函数为
我们现在引入的共轭先验分布,形式为
其中是式(2.146)定义的Gamma分布。这些分布共同给出了一个高斯-Gamma共轭先验分布。
对于这个简单的问题,后验概率可以求出精确解,并且形式还是高斯-Gamma分布。然而,为了讲解的目的,我们会考虑对后验概率分布的一个分解变分近似,形式为
注意,真实的后验概率分布不可以按照这种形式进行分解。最优的因子可以从一般的结果(10.9)中得到,如下所述。对于,我们有
对于配平方,我们看到是一个高斯分布,其中,均值和方差为
注意,对于,这给出了最大似然的结果,其中,精度为无穷大。
类似地,因子的最优解为
因此是一个Gamma分布,参数为
同样的,当时,它的行为与预期相符。
应该强调的是,我们不假设最优概率分布的具体的函数形式。它们的函数形式从似然函数和对应的共轭先验分布中自然地得到。
因此,我们得到了最优概率分布的表达式,每个表达式依赖于关于其他概率分布计算得到的矩。因此,一种寻找解的方法是对例如进行一个初始的猜测,然后使用这个猜测来重新计算概率分布。给定这个修正的概率分布之后,我们接下来可以计算所需的矩,并且使用这些矩来重新计算概率分布,以此类推。由于这个例子中,隐含变量空间是二维的,因此我们可以用图形来说明后验概率分布的变分近似过程。我们画出了真实后验概率的轮廓线和分解近似的等高线,如图10.4所示。
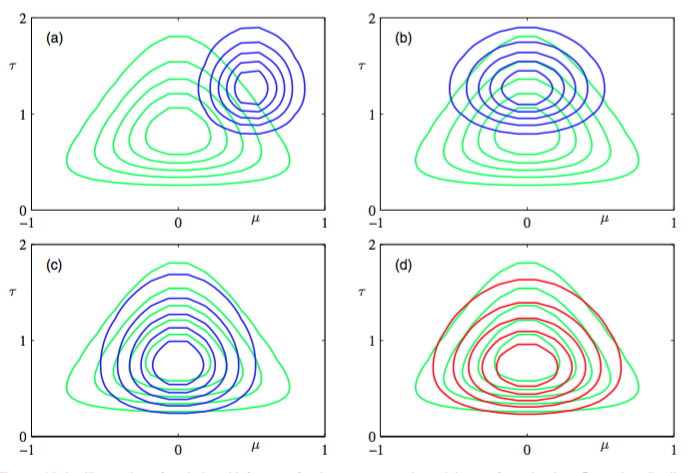
图 10.4 一元高斯分布的均值和精度的变分推断的例子。真实后验概率分布用绿色曲线表示。(a)初始的分解近似,用蓝色曲线表示。(b)重新估计了因子之后的结果。(c)重新估计了因子之后的结果。(d)最优分解近似的轮廓线,其中迭代方法收敛,用红色表示。
通常,我们需要使用一种迭代的方法来得到最优分解后验概率分布的解。然而,对于我们这里讨论的非常简单的例子来说,我们可以通过求解最优因子的方程,得到一个显式的解。在做这件事之前,我们可以通过考虑无信息先验来简化表达式。无信息先验分布中,。虽然这些参数设置对应于一个反常先验,但是我们看到后验概率分布仍然具有良好的定义。使用Gamma分布的均值的标准结果,以及式(10.29)和式(10.30),我们有
之后,使用式(10.26)和式(10.27),我们得到了的一阶矩和二阶矩,形式为
现在,我们可以将这些矩代入式(10.31),然后解出,可得
对于高斯分布的贝叶斯推断的可理解的介绍,包括与最大似然方法的相比的优势的讨论,可以参考Minka(1998)。